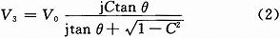
式中:C为耦合度;V3为耦合端输出电压;V0为耦合器输入端电压。显然,当长度为90°时,tanθ=0,V3=CV0,耦合端信号最大。而该耦合器的长度为92.4°,基本上符合耦合器的基本理论,这个耦合度的数值应该和S31的数值接近。从后面的分析中可以看到,这个数值和矩量法计算的结果是基本一致的。另一个重要的参数是S41这个参数在理想耦合器理论中为0,但实际中显然不为0,因为奇偶模的不平衡性,其性能有可能变差,甚至很差。另外用传输线等效理论分析办法,分析输入S11参数,但这种办法也只能是粗略的分析,这是由于微带线传输的奇偶模相速度不平衡,奇偶模分量也很难计算。不过因为耦合度比较低,可以假设1端口到2端口的耦合线为一根独立的无耗传输线来计算。1,2端口的阻抗均是50Ω。利用公式(3)可以计算的结果是,Zin1=44.25-j10.24 Ω,Zin2=30.7+j7.71 Ω,Zin3=37.12+j10.65 Ω。这里的1,2,3指的是图上标的点。用公式(4)可以计算得到Γ=0.13+j0.138,S11=-14.4dB,从这个数据上看来阻抗匹配不是很好。现在的理论分析结果用以和后面的矩量法计算结果进行比较。
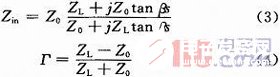
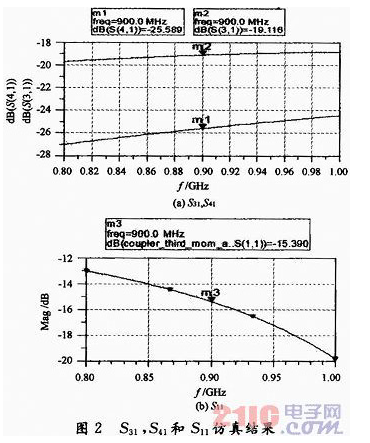
图2(a)是S31和S41的图,在900MHz时S31为-19.116dB,S41为-25.589dB。图2(b)是S11的图,在800MHz~1GHz之间,S11均在-12dB和-20dB之间。从图2上可以看出,这个耦合器的性能并不好。首先是S11在900MHz时仅为-15.39dB,定向耦合器是一个直通的设备,一般来说S11必须要在-30dB以下才合适,否则插入损耗有些过大,对系统有一些损害。另外定向性过低,在900MHz时,隔离度为-25.589dB,耦合度为-19.116dB,定向性只有6dB左右,而且在整个频段,定向性都不超过8dB。这个结果显然比较符合上文计算的结果,S11=-15.39dB接近上文中的-14.42dB,而S31=-19.116dB和最大耦合功率的理论值-19.48dB也比较接近。