也就是说Rx和分压器2上的电压都增加了n/k(=4)倍,因此这时Rx上的功率为
P2=(n/k)2P1=16 P1
电位差计的测量结果是
(n/k)I2’R2=I2’ R2/4
由式(6),得到
I2’R2=A+α (7)
式中 α—由电阻Rx负载效应引起的电位差计读数增量。
由式(2)、(5)、(7)经简化可得
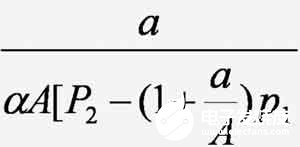
(8)
取不同的 k值即k=1,2,3,。..,n-1,则可按式(8)得到一组η值,取其平均值做为测量结果时可进一步提高η的测量准确度。
四、误差分析
本测量方法的主要误差源分析如下。
1 电流测量误差
在测量原理中,利用了式(6),担实际上由于电流的测量误差,此条件不能满足,即实际情况是
I2=n/k(1+Δ)I1
式中 Δ—测量电流的误差。
于是式(8)为
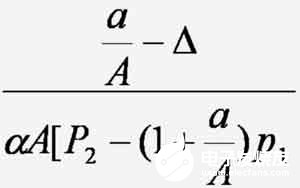
由于在改变电流时电压表的读数不变,因此Δ的主要来源是分压器2各元件的负载系数的负载系数差异,但只要在工作条件下自校并对分压比俾修正,把它减小到10-6以下是容易办得到的,若改用直流电流比较仪提供测量用电流,则误差还可减少。
2 分压器1的误差
分压器比的误差有两个因素,第一是电阻元件自身对名义值的偏离;第二是分压器的负载效应,这是由于分压器电阻都是相同的规格,因此负载效应很小;第三是可以在工作电压下测量其分压比,从而进一步消除它的负载效应。因此把分压比的误差减小到10-6。