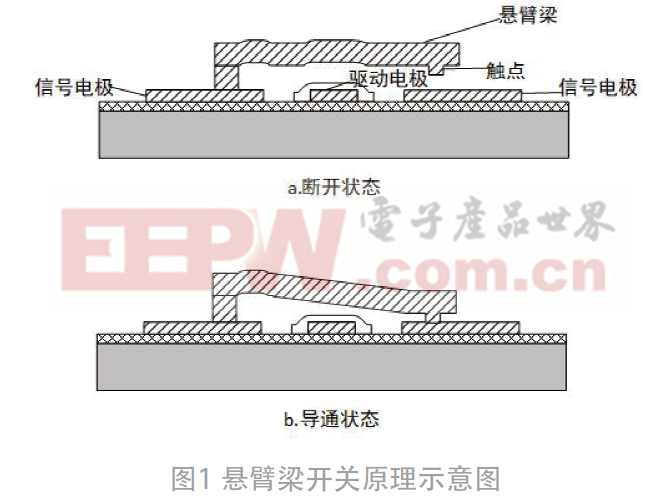
由射频微系统的相关知识可知:梁的不稳定状态g和驱动电压Vp分别为[5]:

其中:g为悬臂梁到驱动电极之间的间隙,g0为初始间隙。悬臂梁宽度ω,驱动电极宽度W。
2 一字梁的弹性系数
当驱动电压升到Vp 时,悬臂梁在静电力作用下会快速下拉,此时触点金属和信号电极接触,则信号导通。从式(2)可以看出,悬臂梁的弹性系数 k是计算悬臂梁的驱动电压的关键,接下来我们对弹性系数的 k值进行分析。
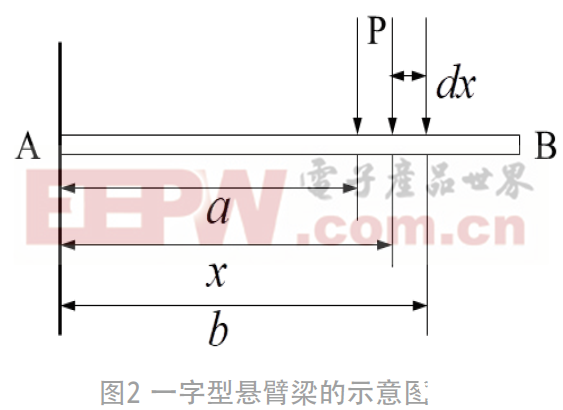
如图2 所示, 当一字型悬臂梁的任意位置受到均布载荷时[6],由材料力学知识可得: dP =ξ dx ,
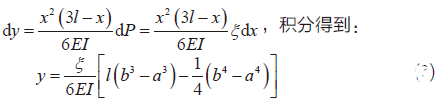
其中:ξ为单位长度的载荷大小,y为悬臂梁的挠度,E为梁材料的弹性模量,l为梁的长度,I为转动惯量,对于矩形截面,则I=ωt3/12,其中t为梁的宽度。
在静电力载荷的作用下悬臂梁的变形程度很小,可以用胡克定律F=kx来描述,即
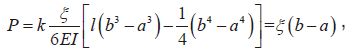
解得:
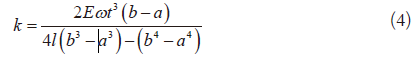
当载荷均布在整个梁上时, 即 a=0、b=1,k=2Eωt3/3l3。对于共面波导(CPW)传输线,载荷在梁下方正中间位置,宽度为梁长的1/3,即a=l/3、b=2l/3,此时k=54Eωt3/69l3。将k带入式(2)可以得到理想情况下的驱动电压公式。
3 开关的机电仿真
由于CPW的传输优势,RF MEMS开关通常选择CPW的传输模式[7],但是k的增加导致了驱动电压的增加,所以在CPW传输模式中设计具有低弹性系数的悬臂梁显得至关重要。
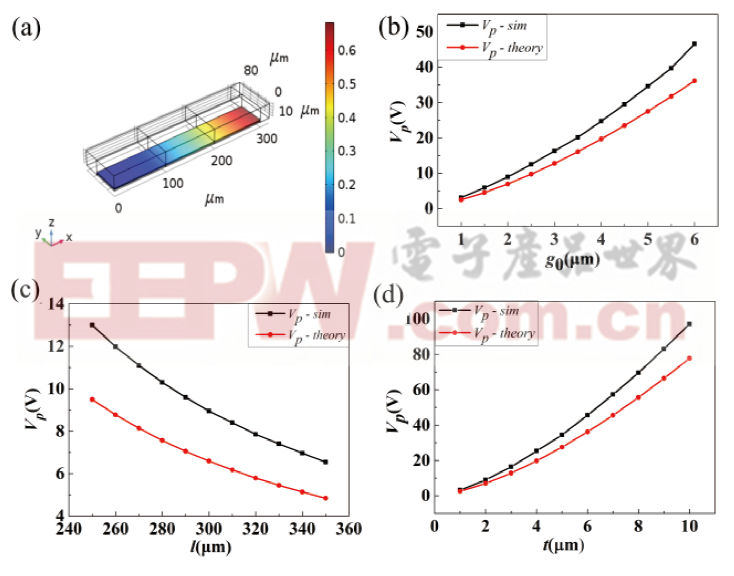
图3为一字型悬臂梁驱动电压的仿真结果。当梁的长度l=300 μm、梁的宽度t=2 μm、悬臂梁到驱动电极之间的初始间隙g0=2 μm时,悬臂梁在9 V驱动电压下的Z向位移图如图3(a)所示。图3(b)~3(d)分别为改变不同参数情况下得到的驱动电压图,从中可以得到理论和仿真结果的变化趋势一致,但在数值上理论计算小于仿真结果,主要原因是仿真时可在梁的周围设置空气层,梁产生形变过程中会影响空气层中电场分布,因此增大了驱动电压的仿真结果。