服从正态分布时,不同应力下分布参数的均值比值和均方差比值近似相等,即:μT1/μT2 = σT1/σT2 ≈ 2.28,μT2/μT3 = σT2/σT3 ≈ 3.4,μT1/μT3 =σT1/σT3 ≈ 7.8,即样本在加速退化过程中的退化机理保持一致,符合加速模型的基本假设,外推出MEMS陀螺仪在正常使用条件下的分布参数μ0和σ0,因此给定时间t的样本可靠度为:
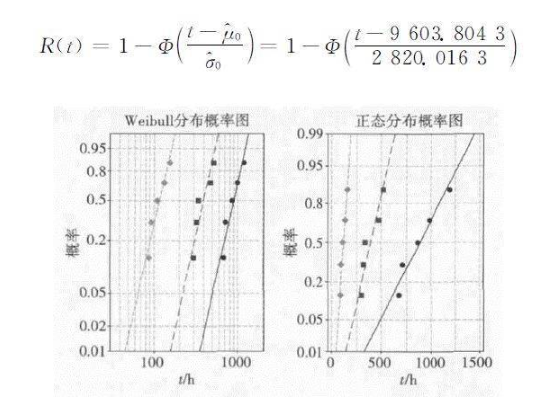
图5 不同应力下退化伪失效时间的分布假设检验
服从Weibull分布时,形状参数近似相等,即样本在加速退化过程中退化失效机理保持一致,符合加速试验的基本假设,外推样本在正常使用条件下的分布参数:m0 = 4.5662,η0 =11101.72,因此给定时间t样本可靠度为:
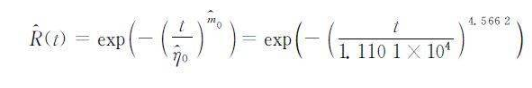
3.2 基于退化量分布的拟合方法
对不同温度应力,不同测量时刻的参数退化量分布假设检验,结果如图6所示,不同时刻样本退化量基本服从正态分布和Weibull分布,且不同时刻所服从的Weibull分布形状参数m近似相等。
服从正态分布时,均值与均方差随时间的变化曲线如图7所示,在不同温度应力下参数退化量的均值与均方差是时间的线性函数,且求得的方程系数随应力增加而增加。
假设样本参数退化量均值与均方差方程系数与温度的关系满足Arrhenius加速模型,分布参数与时间、温度的关系为:
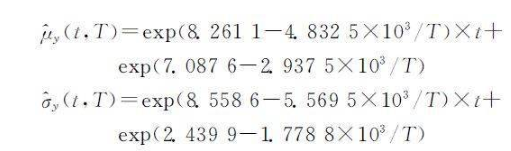
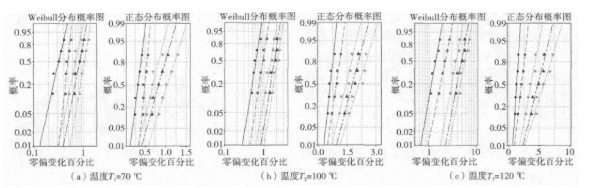
图6 不同温度应力,不同测量时刻参数退化量分布假设检验图
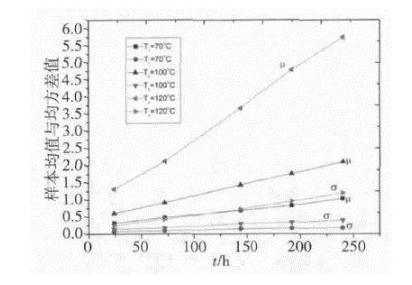
图7 不同温度应力下参数退化量均值与均方差曲线
求得正常使用条件(T0 = 25 ℃)下均值μ y0 和均方差σ y0 与时间的关系,因此给定时间t,MEMS陀螺仪基于参数退化量分布的可靠度函数为: