
由式(8)可见,第k段的非零值时区为(kT,(k+1)T_),即各时段非零值区间互不重叠,对hk(t)关于k求和,得开关电容电路(对外)的单位冲激零状态响应h(t)为:
特别注意,求和式是一周期为2T的周期方波p(t)与单位阶跃信号ε(t)的乘积,对上式取Fourier积分变换即得到开关电容电路系统频谱函数(用j表示虚数单位,下同):
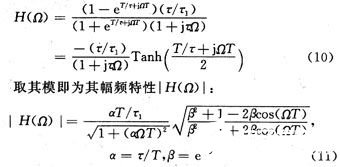
也可以根据式(1)定义的周期为2T的开关方波信号p(t),将式(9)改写为:
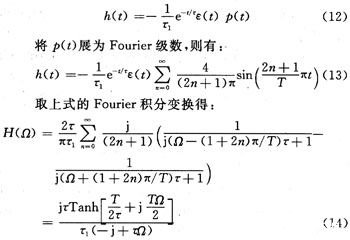
易证式(13)与式(10)完全一致,故其幅频特性∣H(Ω)∣仍与式(11)相同。
3 频域法特性分析
开关周期切换,形成的RC并联支路对外电路的等效电流ie(t)为:
上式说明,Ie(Ω)是输入电流频谱I(Ω)周期延拓的组合,周期为Ω0=2π/T。各电流分量流过RC并联支路时的电压为相应电流分量与RC支路阻抗(R/(1+jωτ),ω=Ω(2n+1)π/T)的乘积,于是输出电压频谱U(Ω)为:
为求系统频谱函数,取i(t)=-ui(t)/R1=-δ(t)/R1,I(Ω)=-1/R1,得到系统频谱函数:
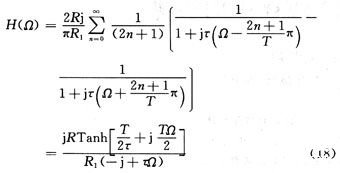
其中R/R1=τ/τ1,结果与式(14)一致,幅频特性∣H(Ω)∣仍与式(11)相同。
4 结 语
给定图1(a)电路参数τ和τ1,选择α=τ/T分别取不同值时,根据式(11)做出的归一化幅频特性曲线如图2所示,结合对式(11)做深入分析表明:
(1)α=τ/T较大时电路是梳齿幅度按奇数倒数规律衰减的梳状滤波器,通带中心频率(梳齿)为:
此时图1(a)电路允许f=fT,f=3fT,f=5fT,…等频率成份通过,且随着频率的升高,输出幅度按奇数倒数规律逐渐减小。
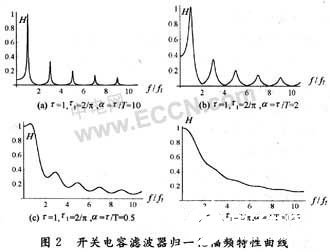
(2)α=τ/T较大时,f=(2n)fT(其中n=0,1,2,…)是系统的阻带中心频率,落在这些频点上的信号将获得最小传输系数,最小传输系数(即梳状滤波器幅频曲线谷底高度)为: