![]()
因此,此费用的变化率是:
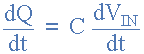
但DQ / dt是电容器电流,I:

从中我们可以得出运算放大器微分器的理想电压输出为:
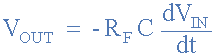
因此,输出电压Vout为常数–Rf*C乘以输入电压Vin相对于时间的导数。负号(–)表示相移180°,因为输入信号连接到运算放大器的反相输入端子。
最后要提到的一点是,与以前的运算放大器积分器电路相比,基本形式的运算放大器微分器电路有两个主要缺点。一个是如上所述的,它在高频下会遭受不稳定的影响,另一个是,电容性输入使其非常容易受到随机噪声信号的影响,并且源电路中存在的任何噪声或谐波都将比输入信号本身被放大更多。这是因为输出与输入电压的斜率成正比,因此需要一些限制带宽的方法以实现闭环稳定性。
运算放大器微分器波形
如果我们将持续变化的信号(例如方波,三角或正弦波类型的信号)施加到微分放大器电路的输入,则最终的输出信号将发生变化,其最终形状取决于电阻的RC时间常数/电容器组合。
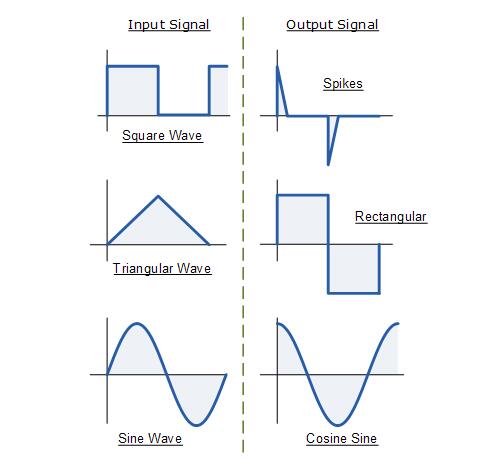
基本的单电阻器和单电容器运算放大器微分器电路由于上述两个固有的错误(“不稳定”和“噪声”)而没有广泛用于改革微分的数学函数。因此,为了降低电路在高频下的整体闭环增益,需要在输入端添加一个额外的电阻Rin,如下所示。
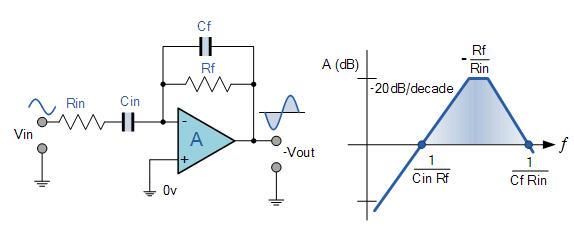
添加输入电阻器R IN限制了微分器以Rf/ R IN的比率增加的增益。该电路现在在低频下就像一个微分器放大器,而在高频下像一个具有电阻反馈的放大器,可以提供更好的噪声抑制。
通过将电容器Cf与微分器反馈电阻Rf并联连接,可以实现更高频率的附加衰减。这样就构成了有源高通滤波器的基础,正如我们之前在滤波器部分所看到的那样。