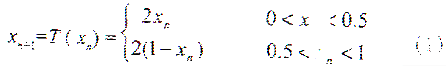
这一映射可以看到由两步组成:先将区间[0,1]伸长2倍,然后再压缩成原区间[0,1]。如此反复迭代操作,最终导致相邻点的指数分离,从而进入混沌状态。这种映射对初始值(系统的输入信号)的放大与通常的线性放大方法不同:线性放大倍数为一常数,而且受工作范围限制;而处于混沌状态的帐篷映射系统,是在有界的区间内,迭代1次将信号放大2倍,反复有限次迭代后,可以将微弱信号放大到可观测的水平,而不会出现溢出再现象。显然,这是一种非线性放大。帐篷映射系统的输入值Vin对应于系统的初始状态x0。x0可以二进制小数表示:

为了得到离散帐篷映射的迭代输出与x0的关系,引入另一种非线性映射——离散贝努利移位是映射:

这一映射的作用是每迭代一次,就将二进制位t1、t2、t3、……向左依次移出一个二进制位,即
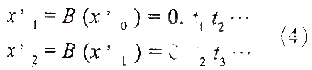
对于贝努利移位映射,令bn=sgn(x“n-0.5),作为贝努利移位映射的第n次迭代输出,由于bn=tn,且bi(i=0,1,2,…)是一个二进制序列;对于帐篷映射,令gn=sgn(xn-0.5),则gi是与bi对应的格雷码序列,即![]()
根据上述和初始时刻x0=x”0=Vi,可得:

因此,通过将帐篷映射迭代输出的格雷码序列gi(i=0,1,2,…),转换成贝努利移位映射的二进制序列bi(i=0,1,2,…),可推算出初始值(输入信号的二进制数字量),即

式(7)中{Vin}表示输入信号的二进制数字量。gi(i=0,1,2,…)就是经过帐篷映射完成了对输入信号的非线性放大和A/D转换的格雷码形式的数字量。
2.2 混沌开关电容A/D转换电路的实现
利用并关电容技术进行电路设计,有其独特的优点:电路的性能与电容无关,只取决于电容之比,两个电容比值的误差小于1/1000,因此电路运算精度高;电路便于实现大规模集成,因而电容体积小、工作可靠、成本低,功耗小(一个开关电容A/D转换器功耗4mW)等。这些优点对模拟式阵列触觉传感器信号采集系统最有利,因此该系统需要大量的ADC。