在模拟集成电路和控制领域常用到的电子器件之一就是运算放大器,在学习的时候对它的理解就是局限于公式推导。在电路调试过程中,遇到调试不顺畅时,有时师傅说增大某某电阻或减小某某电容试试,这种办法有时还真管用,可是不知其精髓,就知道能应急。

运算放大器的原理
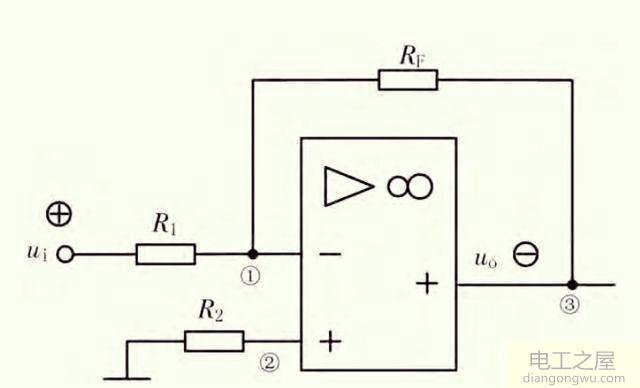
此图是运算放大器电路图,计算和分析此电路。假设此运算放大器的开环放大倍数A=∞、电压约±13V,而饱和输出电压约Uo=±12V。规定此图反馈节点为1。图中的R1、RF分别为1kΩ、2kΩ。R2为平衡电阻,ui=+3V。动态过程:设初始状态uo=0,当ui=+3V时,节点1电压为正,由uo=A×(u+-u-),得uo=A×(0-u1)=-12V。假设此时节点1电压为负,由uo=A×(u+-u-),得uo=A×(0-u1)=+12V。于是uo的电压从-12V到+12V过渡,经过-6V时则u1趋向于零,且满足uo=A×(u+-u-)。因为A很大,所以可稳定在-6V。
当某时刻uo受扰动uo变为-6(+),则u1趋向于0(+),由uo=A×(u+-u-),则uo趋向于-12V,输出减小,当uo达到-6(-)时,则u1趋向于0(-),由uo=A×(u+-u-),则uo趋向于+12V,输出增大,最终维持在-6V,达到动态平衡。由此可见,运算放大器的工作特性由uo=A×(u+-u-)来决定,可将此式视为运算放大器的本质公式,其本质就是差分放大。即输入增大,输出反相增大,同理可得,输入减小,输出反相减小。类似小时候玩的跷跷板,一头翘起另一头下降,于是引出了运算放大器的杠杆原理。在运算放大器的线性区,视运算放大器的输入端ui和输出端uo为杠杆两端,视杠杆支撑点为u1,如图所示(A)。
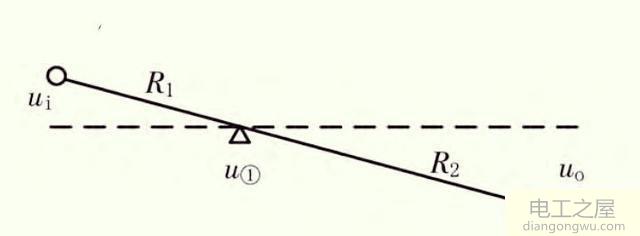
输入、输出与阻抗值(臂长)成正比,把此现象叫运算放大器的杠杆原理。对于此图来说,输入增大,输出反相增大,可理解为滞后180°。而现实中用到的运算放大器开环增益并不是无穷大,一般情况约10^5。
当运算放大器进入饱和区工作时,此时输入ui、参考点u1视为杠杆的两端,而输出uo视为杠杆的支撑点,如图所示(B)。
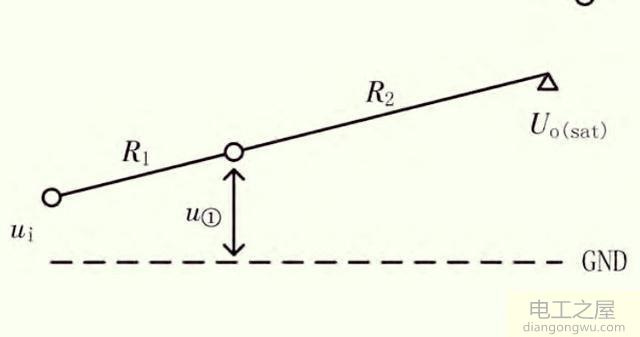
输入与参考点电压u1成正比,视为运算放大器的杠杆原理。一般情况下,运算放大器对应的类型如图(A)的杠杆原理,比较器类型的对应如图(B)的杠杆原理。
实际中运算放大器的开环增益并不是无穷大,而是约为10^5,其中速度与精度的要求往往相互矛盾。高速度要求的是高单位增益频率,而高精度要求的是高直流增益,因此在同一个运算放大器要实现高速度和高精度难度大。由于某些运算放大器的频率特性并不是很好,在中高频时其开环增益有限,由其本质公式可知,得知其虚短效果不佳,故开环增益越大,则调节器就精准。