简单理解积分电路与微分电路
积分电路

积分电路是一个可以把矩形波转化为锯齿波或三角波的简单电路,Uo的电压取自C1的两端,因此电压不能突变,我们可以从公式上这样理解
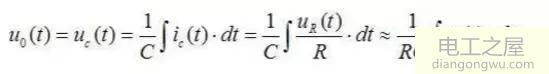
上式表明,输出电压uo(t)与输入电压ui(t)近似地成积分关系,所以该电路被称为积分电路,下面我们通过简单的实验数据来进一步了解一下积分电路,波形是小编实际测试出来的,所以简单粗暴上图:
根据上面的积分电路,当C1固定为4.7uF时,我们通过变换电阻值得到下列波形
R=1K
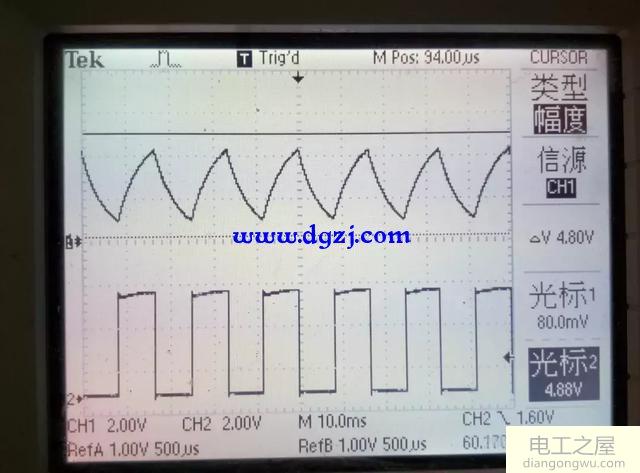
R=20K
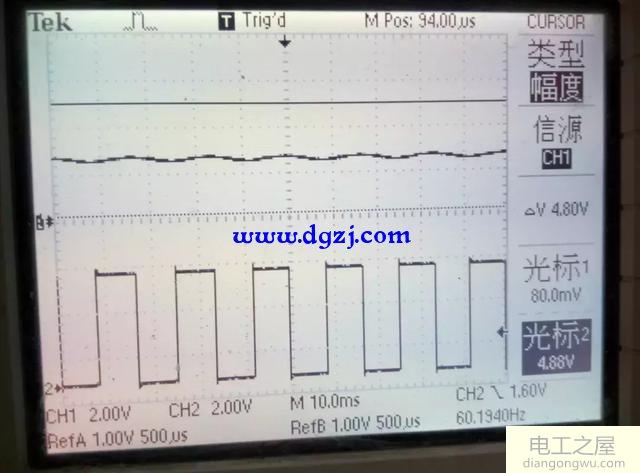
R=150K
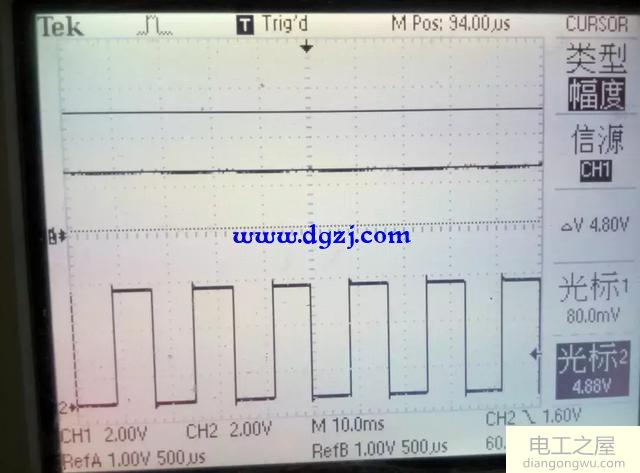
当C1固定为1uF时,我们通过变换电阻值得到下列波形
R=1K
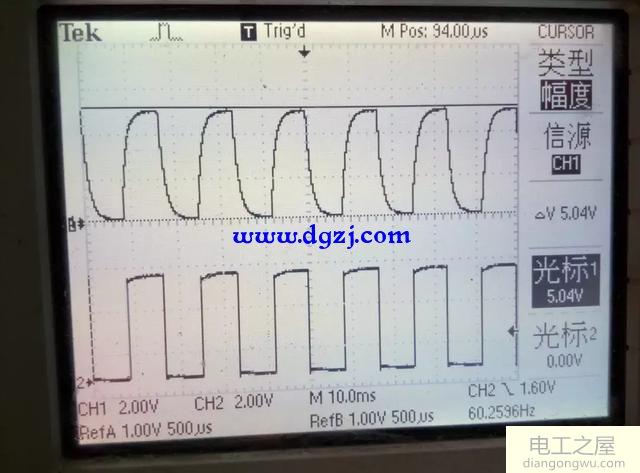
R=20K
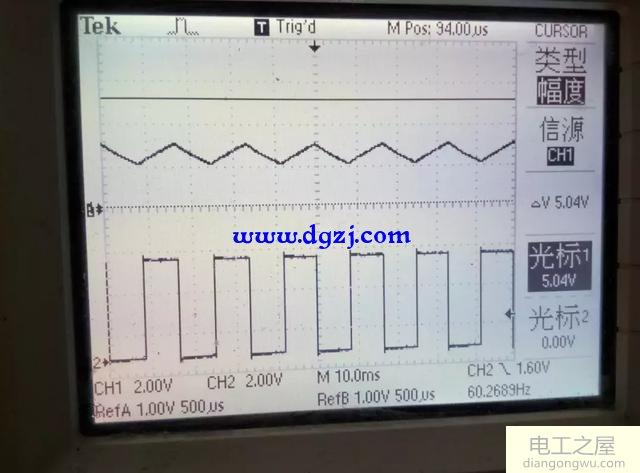
R=150K
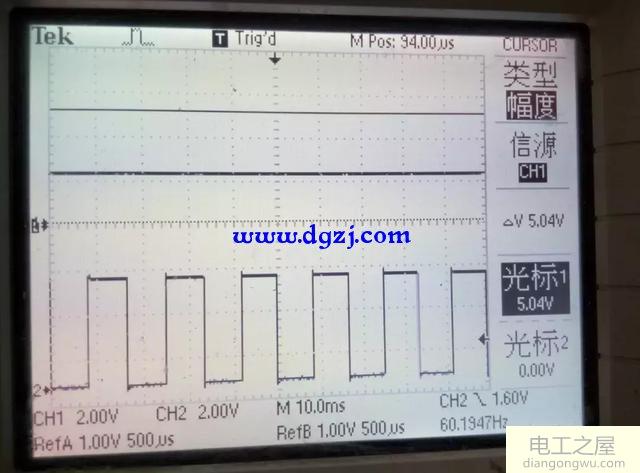
当C1固定为0.1uF时,我们通过变换电阻值得到下列波形
R=1K
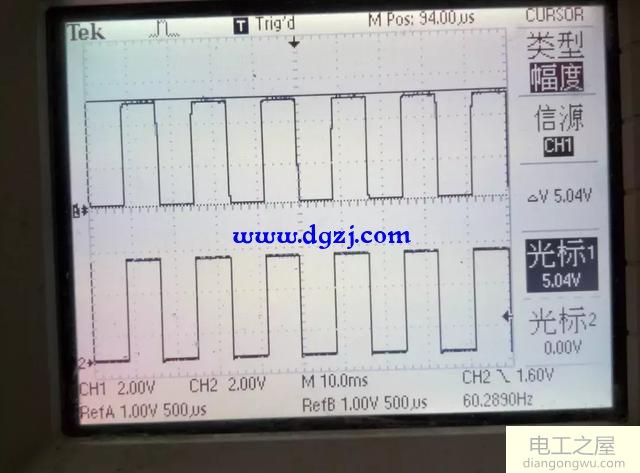
R=20K
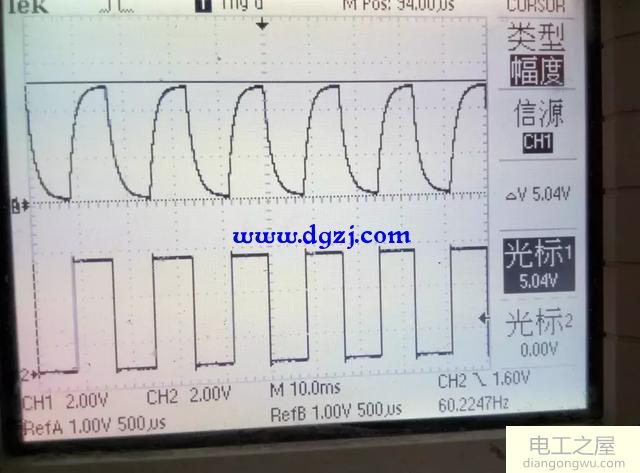
R=150K
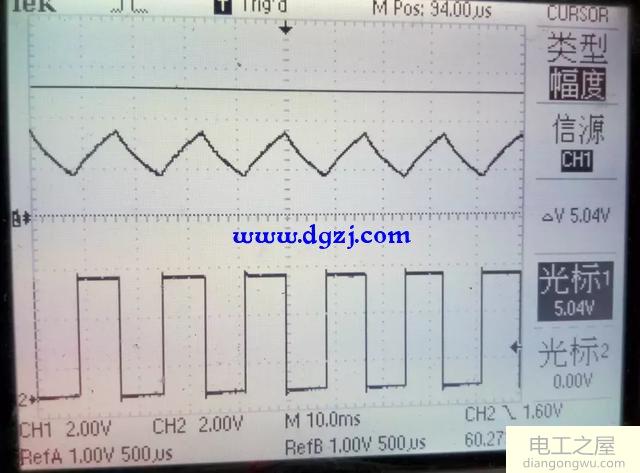
根据这些数据得到以下结论:
电容越大,电容充满电的时间越长,电容两端电压的变化越缓慢,输出电压越平缓,电阻越大,充电电流越小,充电速度越慢,导致输出电压越平缓,而且电阻越大会导致输出电压越低
说到电容充电的快慢,我们可以用另外一个变量来衡量,那就是时间常数τ,这里我们简单了解一下时间函数,方便初学者更充分的去理解。
时间常数τ
当电容器通过一个电阻进行充放电时,必须有一定的时间才能充满电或者放完电。而电容器上的电压不会瞬变,因为必须有一定的时间才能将电荷从一点移动到另一点。串联RC电路的时间常数决定了电容器充电或放电的速率。
RC时间常数是一个固定的时间间隔,它等于串联RC电路中的电阻与电容的乘积。
τ=R*C
τ的单位为秒(S),电容的充电曲线是非线性的,通常将这个5倍时间常数间隔看作是一个电容器完全充电或是完全放电的时间,并称之为过渡时间。即放电时间=充电时间≈5τ。
我们再回过头看一下积分电路,当τ越大时,电容充满电的时间越长,假如矩形波的周期是10ms,电容充满电的时间是100ms,也就是说电容才充了很小一部分的电量就要开始放电了,所以输出的波形会很平缓,因为充放电电压波动很小,同理,当τ很小时,输出的波形则会很接近输入的波形。下面我们再大概了解一下微分电路。
微分电路
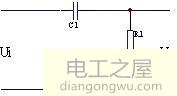
微分电路可把矩形波转换为尖脉冲波,此电路的输出波形只反映输入波形的突变部分,即只有输入波形发生突变的瞬间才有输出。而对恒定部分则没有输出。微分电路的电压取自电阻两端,其公式为
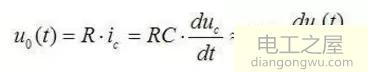
上式说明,输出电压uo(t)近似地与输入电压ui(t)成微分关系,所以这种电路称微分电路。下面我们再用几张简单粗暴的图来了解一下他的特性
当C1=0.1uF时
R1=5K

R1=20K
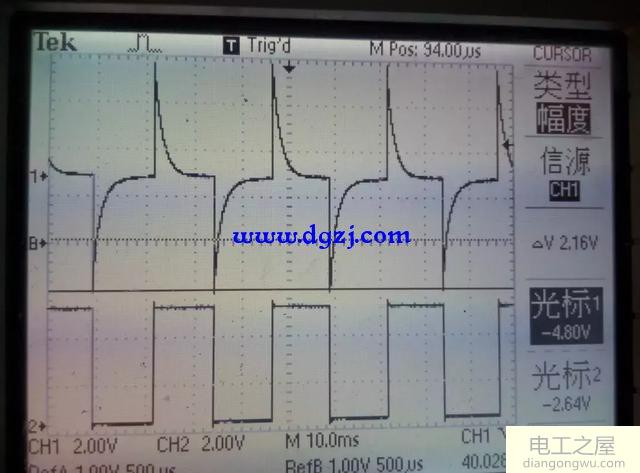
当C1=1uF时
R=5K
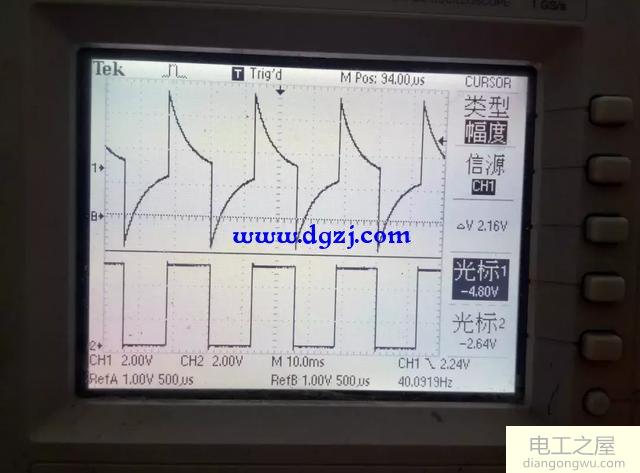
R=20K
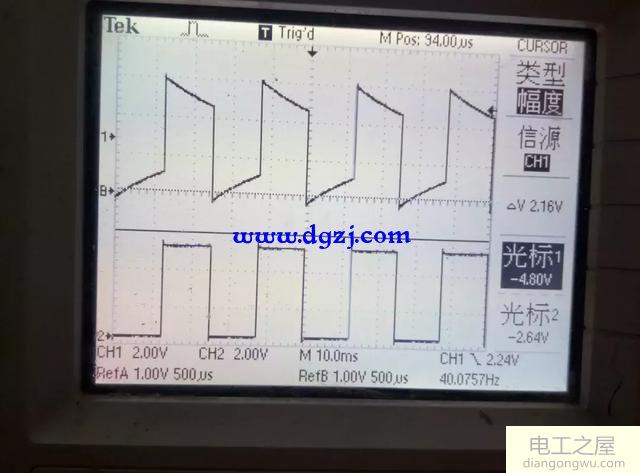
有条件的初学者建议自己动手操作一下,做个类似的小测试,可以加深我们的印象,这里我们就只放几张图片做参考。
通过上面简单的波形我们可以看出τ越大,充电时间就会越长,输出波形越平缓,越接近输入的波形,τ越小,充电时间就会越短,输出波形越尖。