由于一阶低通滤波器的幅频特性下降速率只有-20 dB/10 f,与理想情况相差太大,其滤波效果不佳。为了加快下降速率,使其更接近理想状态,提高滤波效果,我们经常使用二阶RC有源滤波器。采取的改进措施是在一阶的基础上再增加一节RC网络。
电路结构如图1所示,此电路上半部分是一个同相比例放大电路,由两个电阻R1,Rf和一个理想运算放大器构成。R1与Rf均为16 kΩ。下半部分是一个二阶RC滤波电路,由两个电阻R2,R3及两个电容C1,C2构成。其中R2,R3均为4 kΩ,C1,C2均为0.1μF。电路由一个幅度为1 mV,频率可调的交流电压源提供输入信号,用一个阻值为1 kΩ的电阻作为负载。
理论分析
频率特性
二阶低通滤波器电路的频率特性为:

通带电压放大倍数AUP
低频下,两个电容相当于开路,此电路为同相比例器。
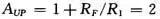
特征频率f0与通频带截止频率fP

Multisim分析
虚拟示波器分析
在Multisim软件的虚拟仪器栏中选择虚拟双踪示波器,将示波器的A、B端分别连接到电路的输入端与输出端(即图1中的1、3节点),再点击仿真按钮进行仿真,得到如下波形。
图2为输入信号频率为1 kHz,幅度为1 mV时二阶低通滤波器电路的输入输出情况。图中横坐标为时间,纵坐标为电压幅度。我们选择示波器扫描频率为1 ms/p。纵轴每格均代表1 mV,输出方式为Y/T方式。幅度大的为输入信号,幅度小的为输出信号。
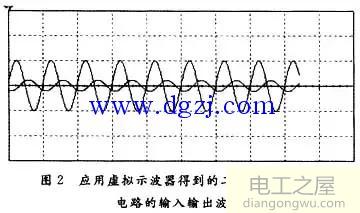
很显然,输出信号的频率与输入信号一致,说明二阶低通滤波器电路不会改变信号频率。从图2还可以看出,在输入信号频率较大(如1 kHz)时输出信号的幅度明显小于输入信号的幅度。而低频情况下的理论计算结果AUP=2;即在低频情况下输出信号的幅度应为输人信号的两倍。很显然,输入信号频率较大时电路的放大作用已经不理想。
调节输入频率,使之分别为800 Hz,600 Hz,400 Hz,300 Hz,200 Hz,150 Hz,1 Hz。由虚拟示波器得到输入频率为1 Hz时的输出电压Uo1=2 mV,即AUP=2,与理论计算值相吻合。而输入频率为150 Hz时Uo2=1.5 mV。此时Uo2最接近截止时的输出电压UP=0.707Uo1=1.414 mV。这说明截止频率fP接近150 Hz。
我们发现,仅通过虚拟示波器分析,既很难得出fP的准确值,也不能直观看出输入信号的频率对电路放大性能的影响,于是用Multisim中的交流分析来精确观察电路的输入输出特性。
交流分析(AC Analysis)
停止Multisim仿真分析(Multisim仿真分析与交流分析不能同时进行),在主菜单栏中simulate项中选择Analysis中的AC Analysis。参数设置如下:起始频率为1 Hz,终止频率为10 MHz,扫描方式使用十进制,纵坐标以dB为刻度,在Output variables中选择输出节点(即图1中节点3),然后点击simulate进行仿真分析,得到电路的幅频特性曲线如图3所示。
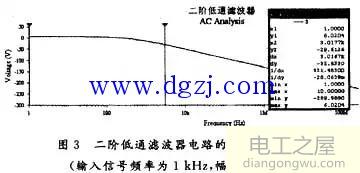
通带电压放大倍数AUP的测量
从特性曲线可以看出,在低频状态下频率变化对AUP的影响不大,频率较大时AUP随频率增加而急剧减小。高频状态下输出电压则接近于0。从对话框中可知纵坐标最大值为6.020 4 dB,即AUP=2,与理论计算值相符。
通频带截止频率fP的测量
fP为纵坐标从最大值(6.020 4 dB)下降3 dB时所对应的频率,即纵坐标为3.020 4 dB所对应的频率。将图3中右侧标尺移至3.020 4 dB附近,选其局部进行放大;再将该标尺精确移至纵坐标为3.020 4 dB处,得到的横坐标为148.495 2 Hz,即fP=148.495 2 Hz。这与理论计算得到的基本一致。
参数扫描分析(parameter sweep)
当某元件的参数变化时,利用Multisim中的参数扫描分析功能可以得到电路输入输出特性的变化情况。
在主菜单栏中simulate项中选择Analysis中的parameter sweep。参数设置如下(以分析C1为例):设备项中选择电容设备,元件名选择C1,参数选择电容量,电容量使用le-006F,le-007F,le-008F三个值。点击more选项,选择AC Analysis(交流分析),再选择节点3作为输出节点。点击simulate进行仿真,得到C1取上述三个不同值时电路的幅频特性曲线(如图4所示)。

图4中,三条曲线由下至上对应的电容分别为le-006F、le-007F、le-008F,对应的截止频率分别为35.550 Hz,148.493 7 Hz,193.375 6 Hz。很显然,C1减小引起电路的截止频率增大,通频带变宽。而C1的变化对电压增益基本无影响。
采用类似方法,我们得到C2,R1,R2,R3和Rf对电路性能的影响如下:C2,R2和R3的变小均会引起电路的截止频率增大和通频带变宽。而C2,R2和R3的变化对电压增益的影响不大。R1与输出电压幅度成反比,Rf与输出电压幅度成正比,但R1和Rf的变化不影响电路的频率特性。