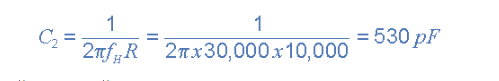
然后,低通级给出截止频率为30kHz所需的R2和C2的值为R =10kΩ和C = 530pF。但是,计算得出的530pF电容器值的最接近首选值是560pF,因此将其替代。
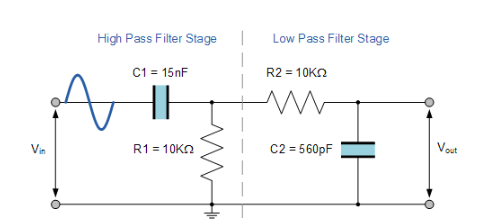
假设电阻R1和R2的值均为10kΩ,高通和低通滤波器的电容C1和C2的值分别为15nF和560pF,那么我们的简单无源带通滤波器的电路给出为。
完成的带通滤波器电路
带通滤波器谐振频率
我们还可以计算输出增益达到最大值或峰值时带通滤波器的“谐振”或“中心频率”(ƒr)点。该峰值不是您可能期望的-3dB上下截止点的算术平均值,而是实际上的“几何”或平均值。这种几何平均值计算为ƒr 2 =ƒc (UPPER) Xƒc (LOWER)例如:
中心频率方程
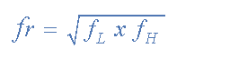
其中,ƒ - [R是谐振或中心频率
ƒ 大号是下-3dB截止频率点
ƒ ħ是上部-3db截止频率点
在我们的上述简单例子中,所计算出的截止频率被发现是ƒ 大号 = 1060赫兹和ƒ ħ = 28420赫兹使用该滤波器值。
然后通过将这些值代入上式得出中心谐振频率为:

带通滤波器摘要
通过将单个低通滤波器与高通滤波器级联在一起,可以制成一个简单的无源带通滤波器。RC组合的上下-3dB截止点之间的频率范围(以赫兹为单位)被称为滤波器“带宽”。
滤波器带宽的宽度或频率范围可以非常小和选择性,或者非常宽且非选择性,具体取决于所使用的R和C的值。
中心或共振频率点是上下截止点的几何平均值。在此中心频率下,输出信号达到最大值,并且输出信号的相移与输入信号相同。
对于这种情况,来自带通滤波器或任何无源RC滤波器的输出信号的幅度将始终小于输入信号的幅度。换句话说,无源滤波器也是衰减器,其电压增益小于1(单位)。为了提供具有大于一的电压增益的输出信号,在电路设计中需要某种形式的放大。