触发器逻辑功能分类及波形图的习题
一.RS触发器
Qn+1=S+RQn
SR=0(约束条件)
二.JK触发器
Qn+1=JQn+KQn
三.T触发器
Qn+1=TQn+TQn
JK触发器的两个输入端连接在一起作为T端,就可以构成T触发器。
当T触发器的控制端接至固定的高电平时,每次CP信号作用后必然翻转成与初态相反的状态。
Qn+1=Qn
四.D触发器
Qn+1=D
关于波形图的习题
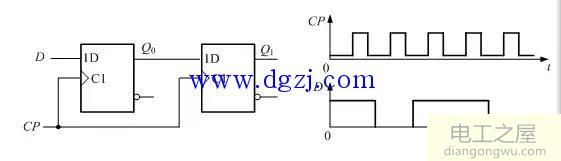
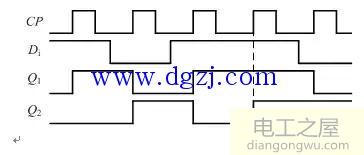
1.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。设触发器的初始状态为Q0 =0,Q1=0。
时序电路分析
1.从给定的逻辑图中写出每个触发器的驱动方程
2.把得到的驱动方程代入相应的触发器特性方程,得出每个触发器的状态方程,从而组成状态方程组。
3.根据电路图写出输出方程。
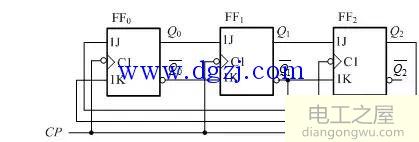
2.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程
(2)作出状态转移表、状态转移图
(3)指出电路的逻辑功能,并说明能否自启动
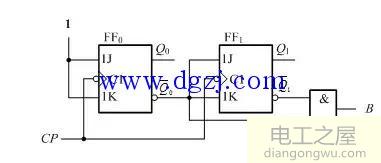
试分析图4-9下面时序逻辑电路
(1)写出该电路的驱动方程,状态方程和输出方程
(2)画出Q1Q0的状态转换图
(3)根据状态图分析其功能
任意进制计数器的构成方法
假定已有N进制计数器,需要得到M进制计数器。这时有M>N和M<N两种情况(M>N这里不做讲解)
M<N时,在N进制计数器的顺序计数过程中要设法跳越N-M个状态,就可以得到M进制计数器了。
方法有置零法和置数法两种。
置零法适用于有异步置零输入端的计数器。它是从S0开始计数并接收了M个计数脉冲以后,电路进入Sm状态产生了一个置零信号加到计数器的异步置零输入端,计数器立刻返回S0状态。这样实现跳越N-M个状态。
置数法是通过给计数器重复置入某个数值来实现跳越N-M个状态,从而得到M进制计数器。
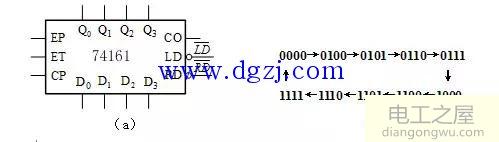
3.十六进制计数器74161的逻辑符号如图4-27(a)所示,功能如表4-1。要求构成十进制计数器,其十个循环状态如图4-27(b)所示。请画出接线图,可以增加必要的门。
时序电路的设计方法
一、逻辑抽象,得出电路的状态转换图或状态转换表
1.分析给定的逻辑问题,确定输入变量、输出变量以及电路的状态数。
2.定义输入、输出逻辑状态和每个电路状态的含义,并将电路状态顺序编号。
3.依题意列出电路的状态转换图或状态转换表。
二、状态化简
若两个电路状态在相同的输入下有相同的输出,并且转换到同一个次态去,则称这两个状态为等价状态。
状态化简的目的在于将等价状态合并,以求得最简的状态转换图。
三、状态分配
时序逻辑电路的状态是用触发器状态的不同组合来表示的。需要确定触发器的数目n。因为n的触发器共有2n种状态组合,所以为获得时序电路所需的M个状态,必须取2n-1<M≤2n。
其次,要给每个电路状态规定对应的触发器状态组合。
四、选定触发器的类型,求出电路的状态方程,驱动方程和输出方程
五、根据得到的方程式画出逻辑图
六、检查设计的电路能否自启动
可以利用无关项检查能否自启动,将无关项代入状态转换图当中。
4.试用D触发器设计一个同步五进制加法计数器,要求写出设计过程。

答案
1.解:

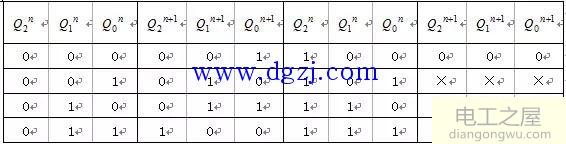
(3)列出状态真值表
(4)画出状态转换图
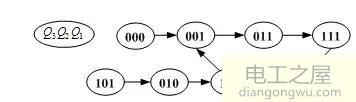
(5)具有自启动能力的同步五进制加法计数器。
3.解:
当Q3Q2Q1Q0=0000时跳到0100,然后记数到1000时又跳到1100,故
(1)从Q2Q1Q0=000译码(起跳);
(2)置入数据为D3=Q3,D2D1D0=100
(3)接线图

4.解:
(1)状态转换图
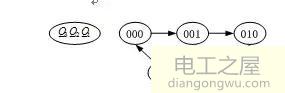
(2)状态真值表
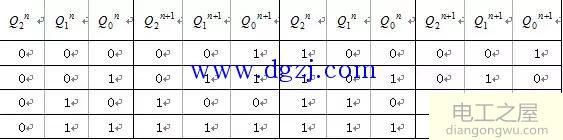
(3)求状态方程
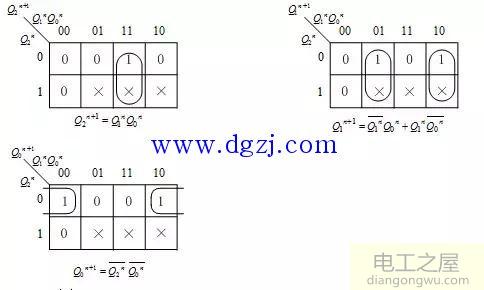
(4)驱动方程

(5)逻辑图
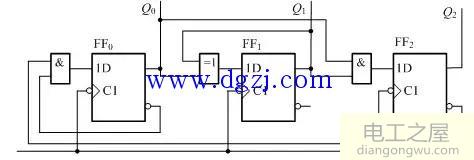
(6)自启动检验