LLC串联谐振电路分析
根据电路原理,电感电容串联或并联可以构成谐振电路,使得在电源为直流电源时,电路中得电流按照正弦规律变化。由于电流或电压按正弦规律变化,存在过零点,如果此时开关器件开通或关断,产生的损耗就为零。下边就分析目前所使用的LLC谐振半桥电路。基本电路如下图所示:
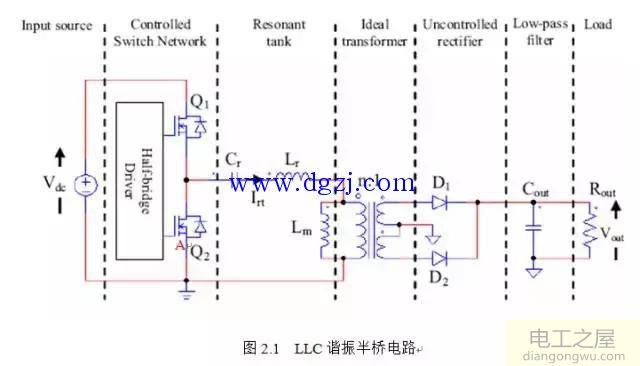
其中Cr,Lr,Lm构成谐振腔(Resonant tank),即所谓的LLC,Cr起隔直电容的作用,同时平衡变压器磁通,防止饱和。
2.1 LLC电路特征
(1)变频控制
(2)固定占空比50%
(3)在开关管轮替导通之间存在死区时间(Dead Time),因此Mosfet可以零电压开通(ZVS),二次侧Diode可以零点流关断,因此二极管恢复损耗很小
(4)高效率,可以达到92%+
(5)较小的输出涟波,较好的EMI
2.2 方波的傅立叶展开
对于图2.1的半桥控制电路,Q1,Q2在一个周期内交替导通,即占空比为50%。所以VA为方波,幅值等于Vin,其傅立叶级数展开为
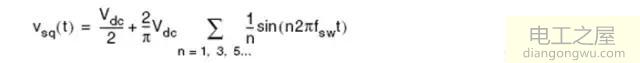
其基波分量为

其中fsw为开关频率,Vo.FHA(t)为谐振腔输入方波电压的基波分量。
相应地,谐振腔输出电压(即理想变压器输出)也为方波
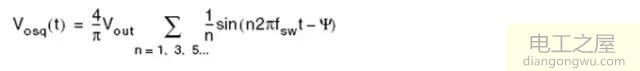
其基波分量为

其中Ψ为输出电压相对输入电压的相移,实际上为零。
2.3 FHA 电路模型
将图2.1所示电路的非线性电路做等效变换,可以得到下图:
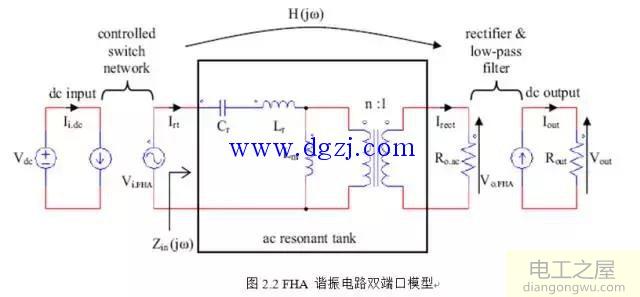
FHA(First harmonic approximation):一次谐波近似原理。该原理是假设能量的传输只与谐振回路中电压和电流傅立叶表达式中的基波分量有关,因此,如果忽略开关频率的影响,则谐振腔被正弦输入电流Irt激励,其表达式为:

其中为输入电流相对输入电压的相移。
相应地,谐振腔输出电流irect为

由于Vo.FHA(t)与irect(t)同相位,所以谐振电路的输出阻抗为

其中Rout为负载阻抗,该阻抗折算到变压器原边的反射阻抗Rac为

所以,谐振腔的输入阻抗Zin(s)为

变压器增益传递函数H(S)为

电压增益M(fsw)为

2.4 电压增益M(fn,λ,Q)分析
对电压增益M(fsw)表达式中的变量进行替换,得到关于fn,λ,Q三个参量的函数,新的表达式为
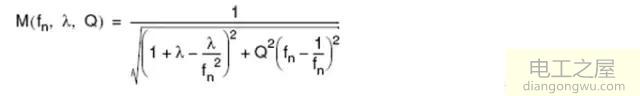
式中参数定义如下:
谐振频率

特征阻抗

品质因数

Lr与Lm电感值比

归一化频率

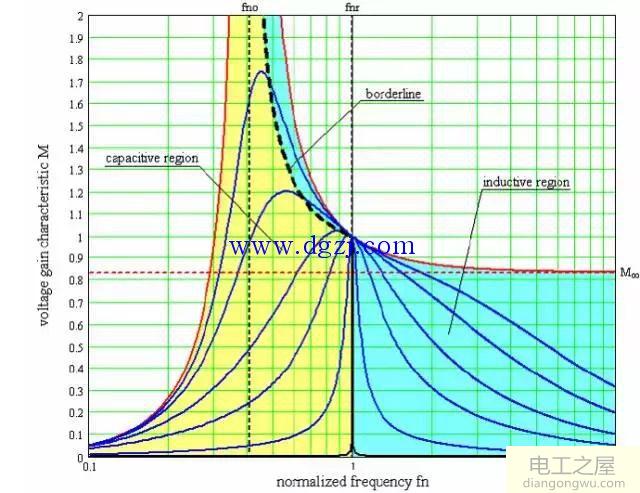
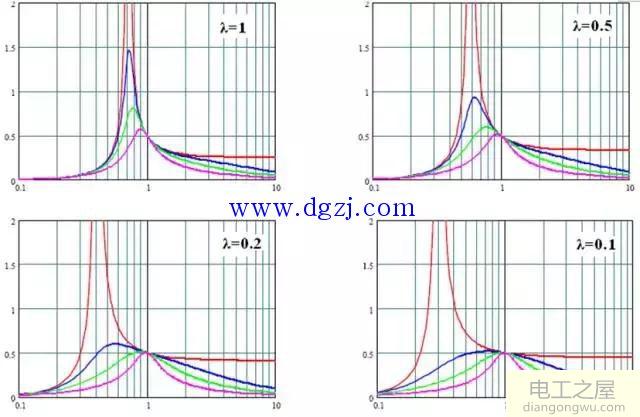
作出λ=0.2时M(fn,λ,Q)曲线簇如下图:
(横轴为fn,纵轴为M)
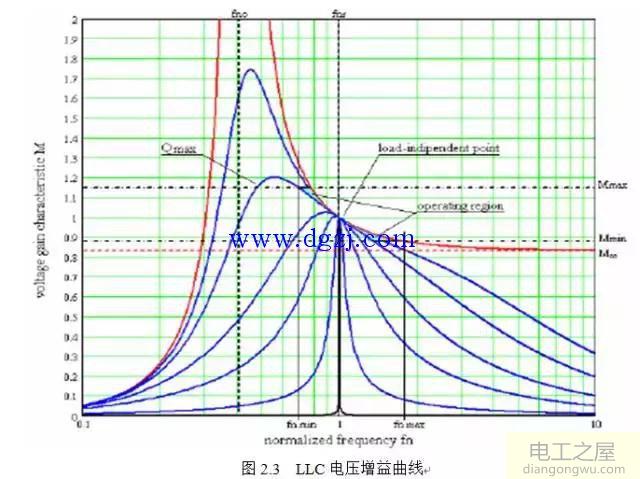
其中红色曲线为空载时(Q=0)的电压增益曲线MOL,随着fn趋向于无穷,MOL逐渐趋向于M∞。

从图中可以看到,对于不同的Q值曲线,都会经过Load-independent point(fr,unity gain),且该点所有曲线的切线斜率-2λ。很幸运,load-independent point出现在电压增益特征曲线的感性区域,这里谐振腔电流滞后于输入电压方波(这个是ZVS的必要条件)。
通过改变输入谐振回路的方波电压频率可以稳定转换器的输出电压:由于工作区域为电压增益特性的感性部分,所以,当输出功率减小或者输入电压增加时,通过提高工作频率来稳定输出电压。考虑到这个问题,如果转换器工作点与load-independent point很接近,那么输出电压的稳定将会与宽负载变化相逆,相应地开关频率变化范围也会很小。
明显地,输入电压范围越宽,则工作频率范围也会相应地变的更宽,因此,很难对电路进行优化设计。这也是目前所有的谐振拓扑结构中普遍存在的缺点。
一般来说,大功率场合一般都有一级PFC电路。对于宽电压输入(85Vac~264Vac),经过PFC之后都会升压到400V,且变化范围不大(10%~15%)。所以对于前端有PFC的LLC电路来讲,LLC输入电压的波动很小,因此上述问题不是很严重。
工作电压变化范围是:最小工作电压由PFC pre-regulator 持续能力决定(hold-up capability)during mains dips;最大工作电压由OVP线路的门限值决定。因此,当输入电压在正常值时,谐振转换器可以在load-independent point优化设计,而最小输入电压during mains dips交给谐振腔自身的提升能力处理。(比如工作点低于谐振点)
另外,还可以得到一个空载时(二次侧Diode不导通)的谐振频率fo

2.4.1 Mmin和fmax的选取
当输入电压Vdc最大,输出负载最小时,电压最小增益Mmin须大于M∞
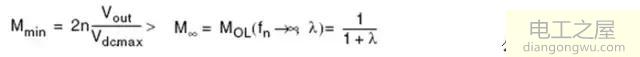
此时最大归一化频率为

2.4.1 Mmax和fmin的选取
当输入电压Vdc最小,输出负载最大时,电压最小增益Mmax

此时最小归一化频率为

关于λ的分析,λ增加相应的变化为:
(1)M-fn平面上的增益曲线向着谐振频率fnr收缩,这同时意味着空载谐振频率fno增加;
(2)空载增益特性渐近线M∞逐渐减小;
(3)每一条增益曲线的最大增益增加。
2.4 归一化阻抗Zn(fn,λ,Q)分析
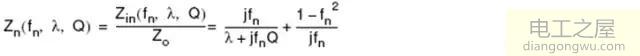
作出λ=0.2时Zn(fn,λ,Q)曲线簇如下图:
(横轴为fn,纵轴为Zn)
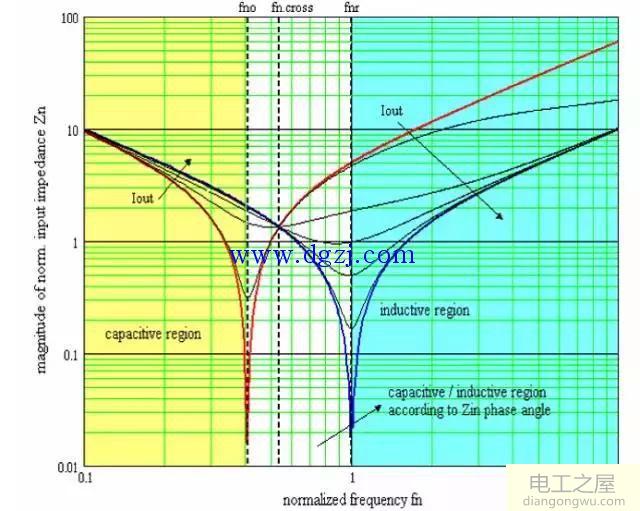
其中,红色和蓝色曲线分别为空载和短路时的归一化阻抗特性曲线,所有的Zn以两个归一化谐振频率fno和fnr为渐近线,且不同Q值的曲线相交于一点,该点的归一化频率fn.cross:

当工作频率大于交叉频率fcross时,输入阻抗随输出电流的增大而减小,当工作频率小于交叉频率时,输入阻抗随输出电流的增大而增大。输出阻抗一直减小。
根据fn可以将整个图分为三个区间
fn
fn>fnr 感性工作区
fno
题外话,通过阻抗特性评估转换器的效率η
输入功率
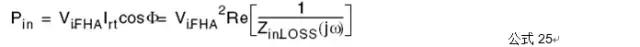
输出功率
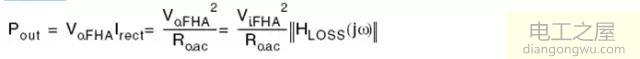
所以效率η

其中Yin.LOSS为输入阻抗的导纳(admittance),等于输入阻抗的倒数(reciprocal)
假设Zn的虚部为零,即Zin为零相位(特征阻抗Zo为真实值,不影响相位),可以从中解出LLC谐振变换器工作于感性和容性区域的临界频率fz,做归一化处理得到:
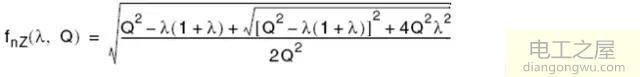
其中fnz只与固定的λ-Q相关,此时输入谐振腔阻抗只有实部(从电源只吸收有用功)。
同时,可以得到最大品质因数

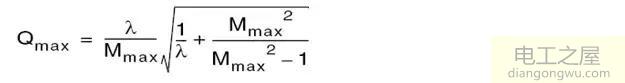
最大品质因数Qmax:当小于Qmax时,对于相同的fn-λ时,谐振腔阻抗呈感性,因此,最大的电压增益Mmax

将Qz(fn,λ)带入M(fn,λ,Q)中,得到如Mz (fn, λ)的表达式

因此,在fnr和fno之间的部分可以画出Mz (fn,λ)以确定感性和容性的分界线borderline,如下图,从图中还可以看到,对于单一Q值曲线来讲,最大的增益点总是落在容性区域