一阶巴特沃斯滤波器设计
根据归一化LPF来设计巴特沃斯型低通滤波器,指的是特征阻抗为1Ω且截止频率为1/(2π)的低通滤波器的数据。用这种归一化低通滤波器的设计数据作为基准滤波器,按照下面的设计步骤,就能够简单的计算出具有任何截止频率和任何特征阻抗的低通滤波器。
2阶归一化巴特沃斯型LPF 截止频率1/(2π)Hz,特征阻抗1Ω
首先选择归一化低通滤波器数据,其次根据需要进行截止频率变换,最后进行特征阻抗变换。
滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器频率的比值M,在用这个M去除滤波器中的所有元件来实现的。

滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器特征阻抗的比值K,在用这个K去乘基准滤波器中的所有电感元件和用K去除滤波器中的所有电容元件来实现的。


如,欲设计一特征阻抗为50Ω且截止频率为300kHz的2阶巴特沃斯型LPF,则根据前面的步骤先求M
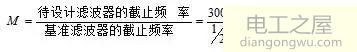
截止频率变换

最终变换结果如图所示
其仿真结果如下所示
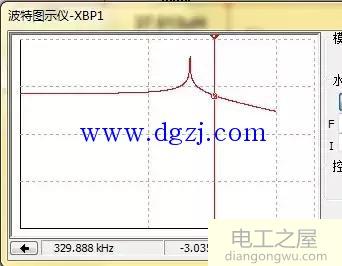
可以看到在-3dB点的频率下降约为330kHZ,基本满足设计要求。
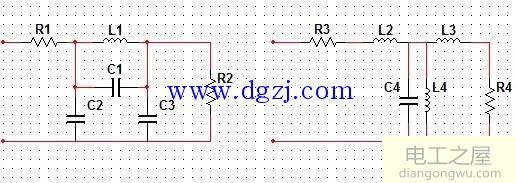
二阶LC低通滤波网络模型
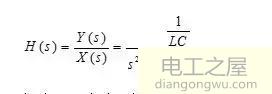
多阶LC滤波器的构成有π型和T型两种。无论怎么连接都可以得到相同的特性,T型的特点是在阻值频率下的输入阻抗大,而π型的特点是输入阻抗小。
二阶LC低通滤波网络模型分析:此网络可以归结为一带初始条件的二阶微分方程
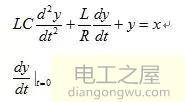
对方程做拉普拉斯变换
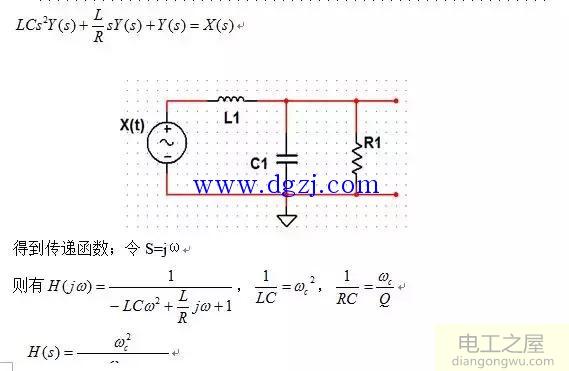
得到传递函数;令S=jω
则有 , ,
Q称为网络的品质因数。通过对不同品质因数Q的二阶LC低通滤波器进行模拟得到幅频和相频特性曲线如下
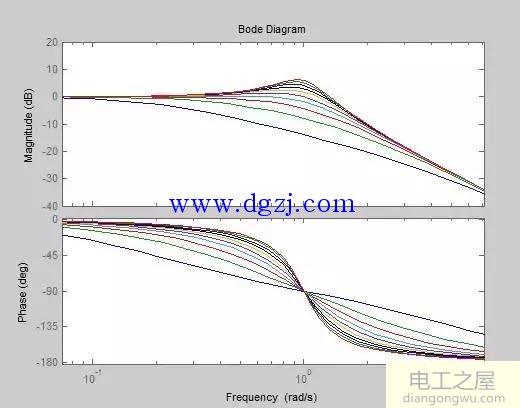
由仿真曲线知道,
当
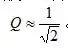
时,Q值越小,低频端输出信号幅度越不稳定,同一输入信号频率下,输出信号的幅度越小,且输出信号的相移比较大。
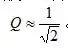
时,输出端没有稳定的幅频特性,在信号源频率等于LC谐振频率时,电路具有谐振性,虽然信号相移不大,但幅度不稳定。
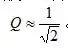
时,电路具有最佳的通带特性,综合考虑其相频特性,在工程应用中设计LC二阶低通滤波网络参数时,应使滤波器品质因数
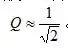
总结:2阶或以上LC滤波电路的设计比较复杂,其N阶的网络模型相当于N阶的微分方程。设计时要根据性能选取适合的函数模型,并进行逼近,得到符合实际元件参数的结果,同时要使滤波器品质因数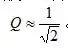 。
。