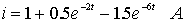二阶电路的零状态响应和阶跃响应讲解
1.零状态响应和阶跃响应
二阶电路的初始储能为零,仅由外施激励引起的响应称为二阶电路的零状态响应。二阶电路在阶跃激励下的零状态响应成为二阶电路的阶跃响应。零状态响应和阶跃响应的求解方法相同。现以图1所示RLC 串联电路为例说明求解方法。
图中激励为阶跃电压,因此电路的初始储能为:
uC(0-)=uC(0+)=0,iL(0-)=iL(0+)=0。
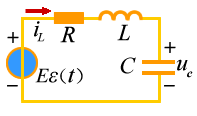
图 1t>0 后,根据 KVL 和元件的 VCR 得以电容电压为变量的电路微分方程:
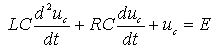
特征方程为;
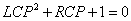
方程的通解求法与求零输入响应相同。
令方程中对时间的导数为零,得方程的特解:
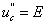
则uC的解答形式为:
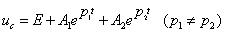
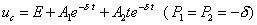
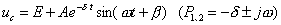
由初值
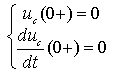
确定常数
电路在阻尼状态和振荡状态时电容电压随时间的变化波形如图2所示,表明电容电压从零上升最后稳定在 E 值。
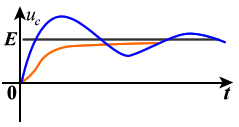
图 22.二阶电路的全响应
如果二阶电路具有初始储能,又接入外施激励,则电路的响应称为二阶电路的全响应。全响应是零状态响应和零输入响应的叠加,可以通过把零状态方程的解带入非零的初始条件求得全响应。
例1 图示电路在 t<0 时处于稳态, t=0 时打开开关 , 求电流i 的零状态响应。
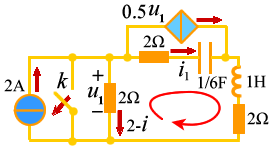
例3 图(a)解:(1)列写微分方程,由 KCL 得:
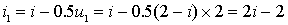
由 KVL 得:
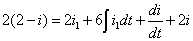
整理以上两个方程得:
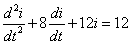
方程为二阶非齐次常微分方程。解答形式为:
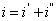
(2)求通解 i'
特征方程为:
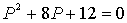
特征根为: P1=-2 , P2=-6
所以
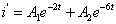
(3)求特解 i ”
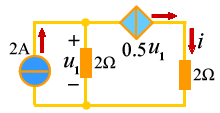
由图(b)所示的稳态模型得:
i=0.5u1,u1=2(2-0.5u1),
解得:u1=2V,i=1A
所以
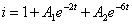
(4)定常数
例3 图(b)
电路的初始值为
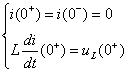
由图(c)所示的0+电路模型得:
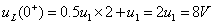
所以
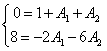
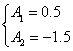
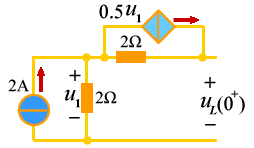
例3 图(c)因此电流为: