1、应该说数字滤波器可以有效减小50Hz工频的干扰,完全消除是不可能的。
2、以20ms为最小单位的整倍数周期滤波,可以有效减少工频的干扰。
我们知道,设计数字滤波器,和模拟滤波器的实质,其实就是求一组系数,逼近要求的频率响应。
模拟滤波器已经很成熟,因此,数字滤波器的设计,将S平面映射到Z平面就型。采用双线性变化法映射,可以避免多值映射产生的混叠现象。但这有个问题就,模拟域和数字域两者的角频率是非线性的。
1.平滑滤波器是数字滤波中较早使用的方法,该算法简单,处理速度快,滤波效果较好,但存在明显不足,通带较窄,影响有用信号的分析,有严重削峰,设计方法略。
然后,我们根据IIR和FIR分两大类。FIR滤波器,可以得到严格的线性相位,但它的转移函数的极点固定在原点,只能通过改变零点位置来改变性能。为了达到高的选择性,必须使用高阶。相同设计指标下,FIR滤波器的阶数是IIR滤波器的5~10倍。而IIR滤波器可以根据模拟滤波器的设计公式,数据和表格,计算量小。
首先介绍IIR类,即两种形式的notch滤波器。
2.陷波器 notch 滤波器
陷波器,是IIR数字滤波器,有signal notch 滤波器,即单一频率陷波器,以及comb notch滤波器,即梳妆滤波器。
陷波器是无限冲击响应(IIR)数字滤波器,该滤波器可以用以下常系数线性差分方程表示:
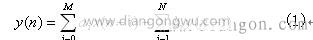
式中: x(n)和y(n)分别为输人和输出信号序列; ai和bi为滤波器系数。
对式(1)两边进行z变换,得到数字滤波器的传递函数为:
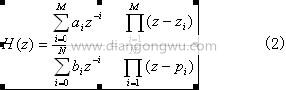
式中: zi和pi分别为传递函数的零点和极点。
由传递函数的零点和极点可以大致绘出频率响应图。在零点处,频率响应出现极小值;在极点处,频率响应出现极大值。因此可以根据所需频率响应配置零点和极点,然后反向设计带陷数字滤波器。