今天小编要和大家分享的是74ls151,74ls138,全加器相关信息,接下来我将从用74ls151实现全加器设计电路,如何用集成二进制译码器74ls138和与非门构成全加器这几个方面来介绍。

如何用集成二进制译码器74ls138和与非门构成全加器
根据全加器的定义可知:
输入为:A,B,Ci其中A,B为被加数和加数,Ci为低位进位数。
输出为:S,Co,其中S为本位和数,Co为高位进位数。
其逻辑关系为:
S=A⊕B⊕Ci
Co=AB+(A⊕B)Ci
计算后,结果用最小项表示为:
S=m1+m2+m4+m7
Co=m3+m5+m6+m7
查询74LS151和74LS138的真值表可知:

(一)74LS138
那么利用74LS138可以得到地址端A,B,Ci对应的所有最小项,然后用两个4输入与非门(74LS20)取得与上面计算得到的对应的最小项和,就能得到想要的结果。可以设计如图1所示电路:
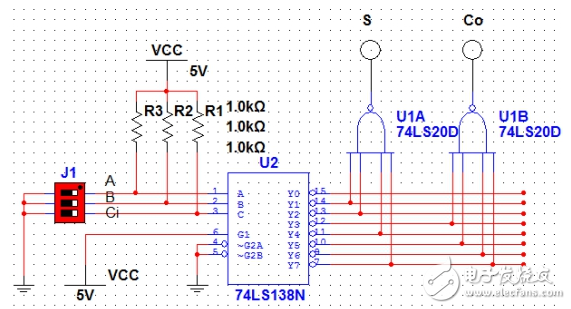
图1
图中,三位拨码开关分别代表A,B和Ci。S和Co是两个灯,代表S和Co的状态,为“1”
时亮,为“0”时不亮。
下面给出{A=1,B=0,Ci=0};{A=0,B=1,Ci=0};{A=1,B=1,Ci=0}和{A=1,B=1,Ci=1}四种输入状态下的S和Co状态。
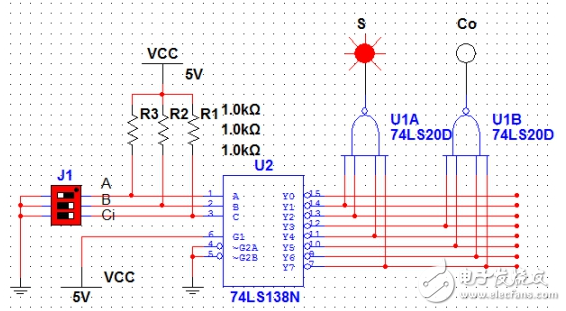
图2(A=1,B=0,Ci=0)
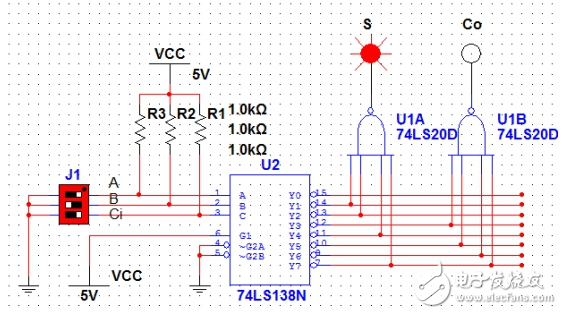
图3(A=0,B=1,Ci=0)
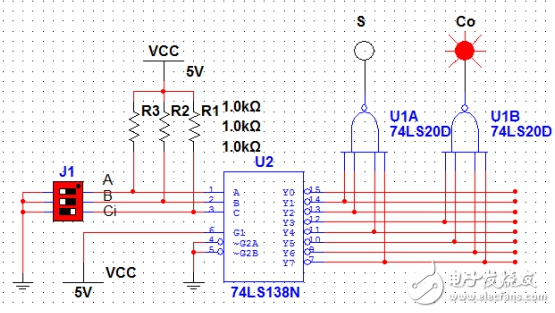
图4(A=1,B=1,Ci=0)
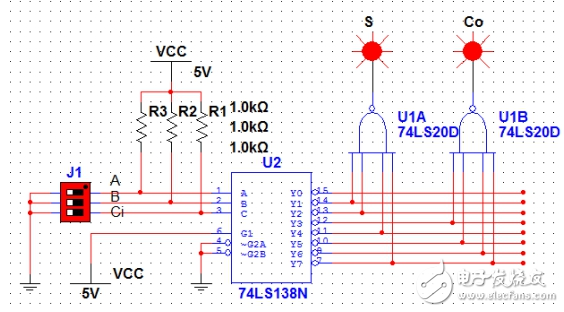
图5(A=1,B=1,Ci=1)
可以看出电路的逻辑关系是正确的。
(2)74LS151
利用74LS151数据选择器可以设计如图6所示电路:
两个74LS151分别得到S和Co;其中U1的数据端配置为D1=D2=D4=D7=1,其余为0;
U2配置为D3=D5=D6=D7=1,其余为0.
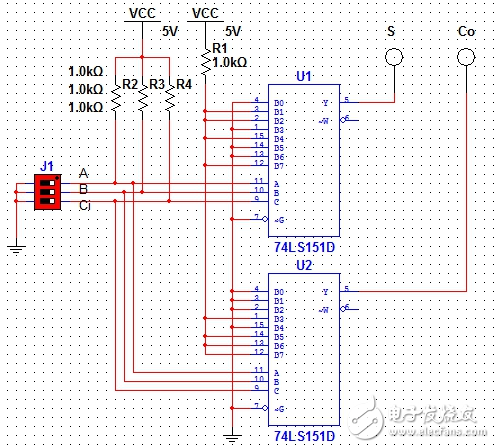
图6
同样,下面也给出{A=1,B=0,Ci=0};{A=0,B=1,Ci=0};{A=1,B=1,Ci=0}和{A=1,B=1,Ci=1}四种输入状态下的S和Co状态。
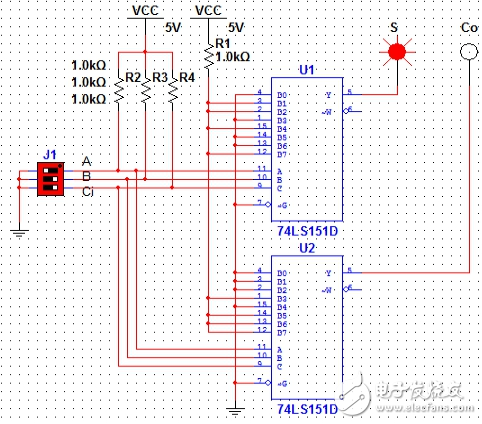
图7(A=1,B=0,Ci=0)
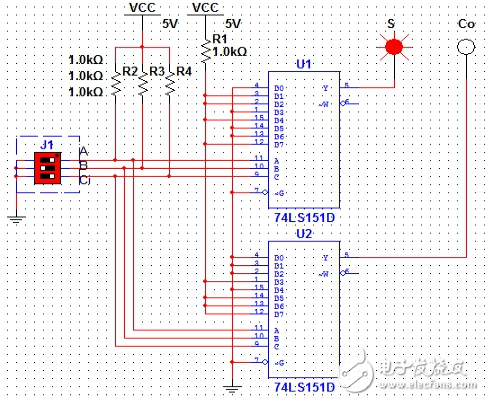
图8(A=0,B=1,Ci=0)
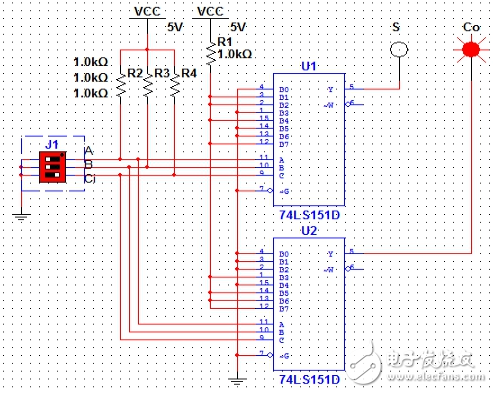
图9(A=1,B=1,Ci=0)
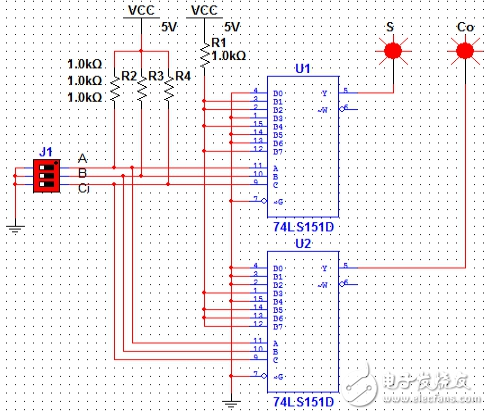
图10(A=1,B=1,Ci=1)
可以看出,电路的逻辑关系也是正确的。
关于74ls151,74ls138,全加器就介绍完了,您有什么想法可以联系小编。