永磁交流伺服电动机在行业应用中,对转矩常数、反电势常数产生很多误解、混淆的原因,并给出了有效解决问题的办法。同时,在应用过程中如何利用好这两个常数,也给出了探讨。为便于工程师理解应用,对GB/T30549-2014中Kt=Ke的结论还给出了详细的演算过程。另外,特别指出永磁交流伺服电动机机械转矩与电磁转矩的区别。
1.选好用好永磁交流伺服电动机的转矩常数和反电势常数(以下称两常数)对于装备制造业用户非常重要。
每一台永磁无刷电动机都具有双重身份,把驱动电流为方波的称为永磁无刷直流电动机(以下称BLDCM),但驱动电流为正弦波的则有几种叫法,在英美的文献中,把这类正弦波驱动的称为“永磁同步电动机(PMSM)”或者“无刷交流电动机(BLACM)”,在日本和欧洲则大多数情况下称为“交流伺服电动机(ACservo)”,国内基本上也多数采用ACservo的名称。本文采用2014年版GB/T30549《永磁交流伺服电动机通用技术条件》(以下称GB/T30549-2014)的叫法—PermanentMagnetACServoMotor(以下简称ACServo)。在采用国际单位制时,BLDCM的两常数是相等的(成立条件:续流回路的电流相对很小可以忽略时),而在ACServo中有的倍数关系,但目前有的工程师还未重视这一区别,另外,不少ACServo公司的产品手册上经常出现两常数相互矛盾的情况,导致行业应用的不少麻烦。为用户理解和应用好两常数起了一定警示作用,GB/T30549-2014对两常数的定义清晰规范,起到了积极的引导作用,但观察近两年国内的ACServo资料,两常数存在问题、矛盾的还是不少,用户碰到这种情况则很困惑、迷茫。在中国制造2025的大背景下,装备制造业(如工业机器人、加工中心、自动化生产线等)的ACServo应用越来越广泛,因此很有必要为ACServo正确选型和应用进一步普及这方面的知识。
2.转矩常数与反电势常数之间的关系
2.1永磁交流伺服电动机的转矩常数Kt
按照GB/T30549-2014条款3.9的定义,是指在规定条件下,电机通入单位线电流时所产生的平均电磁转矩。
也即电机的电磁转矩与电机绕组电流成正比。
Kt=Te/I(N.m/A)(1)
由1.3.1~1.3.4的详细推导演算可以知道GB/T30549-2014标准3.9条款定义的“线电流”指的是“线电流有效值”。
从应用角度来说,客户在为其智能装备进行ACServo规格选型时,所需转矩是最关键指标之一,同时还要考虑留有一定余量,待ACServo装配到相应智能装备之后,再做一次监测计算,确认该ACServo的转矩特性是否真实,与装备的匹配关系是否合理,这样才能确保智能装备大批量生产时的批量合格率,并确保在极端允许工况下设备能可靠运行。
由于ACServo装配到装备上之后,其实际运行时所需最大转矩是非常难以直接测试出来的,那么有何方法可以方便地实时监测到设备上某个轴的负载转矩大小呢?目前大多数智能装备用户都用监测装备上ACServo的绕组电流值,然后乘以转矩常数,就计算出ACServo的机械转矩,然而,由于以下三个原因的存在,导致了这种方法出现错误:
(1)ACServo铭牌上标称的额定电流值一般都是指有效值,而部分驱动器厂商会误认为是峰值;
(2)这样测算出来的转矩实际为电磁转矩,而非机械转矩,前者大于后者,因它含有空载损耗转矩;
(3)转矩常数应该用电流有效值来计算,这才可以得到正确的数值,可有些电机厂商不规范,采用了电流峰值。
电机厂商在测试计算转矩常数时候,有不少会犯一个错误,即工程师错把机械转矩当作电磁转矩了。笔者接触到的几个电机厂商都这样测试转矩常数:在测功机上,通过伺服驱动器设置好ACServo的转速为额定转速值,然后再用测功机逐步加大负载转矩,当负载达到额定转矩时候,记录额定转矩和此时对应的绕组电流。用测试记录的转矩值,除以电流值就得出“转矩常数”。这测试计算方法中,测功机测试到的“额定转矩”其实是机械转矩(TL),但很多电机厂商错误地把它当做“电磁转矩”(Te)直接用于转矩常数的计算,没有注意到需考虑“空载损耗转矩”(T0)的影响,通常认为,三者的关系如下:
Te=TL+T0 (2)
式(2)中,Te为电磁转矩,TL为机械转矩(负载转矩),T0为空载损耗转矩。而T0一般包括两部分:轴承摩擦损耗和风损。
2.2永磁交流伺服电动机的反电势常数Ke
按照GB/T30549-2014的3.10规定,反电势常数是指在规定条件下,电机电枢绕组开路时,单位角速度在电枢绕组中所产生的线感应电动势值。
该标准3.10有规定“对正弦波驱动电机反电动势为有效值”。而PMSM属于“正弦波驱动电机”,因此在PMSM中,需特别注意反电势常数Ke的测试中,所述反电动势应为“线感应电动势有效值”。
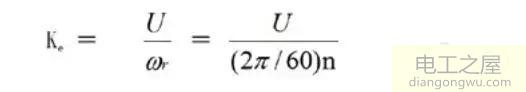
(式中U为反电动势,单位为V;ωr为转子角速度,单位为rad/s;n为电机转速,单位为r/min;Ke单位为V/rad·s-1)
在工程应用中,电动机的转速单位习惯使用每分钟多少转(rpm),很少用角速度,因此工程中反电势常数的常用单位为V/krpm,数值转换关系如下:
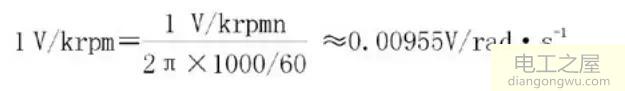
假设以V/krpm为单位的反电势常数为Ken,则有:
Ke=0.00955Ken(V/rad·s-1) (4)
2.3永磁交流伺服电动机Kt和Ke的关系
在永磁有刷直流电机中,当反电势常数和转矩常数的单位都采用国际单位制时,两个常数的数值是相等的。在永磁无刷直流电机(BLDCM)中,两个常数的数值在一定条件下也是相等的,需考虑约束条件“……BLDCM的转矩系数定义为电磁转矩与电枢总电流的比值,而电磁转矩又不完全由电枢总电流产生,使得Kt的值变得不确定,只有续流回路的电流相对很小可以忽略时,Kt的值才是确定的并与Ke相等”。
在ACServo中,反电势常数和转矩常数也都是由永磁体产生的气隙磁通大小,以及定子绕组有效串联匝数的乘积决定的(这个乘积称为磁通链),所以它的两常数也存在确定的数值关系。GB/T30549-2014十分清晰地总结出了这样的数值关系:理想情况下,当采用国际单位制(SI)时,对正弦波驱动的电机,转矩常数Kt和反电势常数Ke有如下关系,

式(5)的数值关系详见如下2.3.1~2.3.4的推导演算。
2.3.1计算基础
查阅电机电磁计算基本公式可知,永磁交流伺服电动机相感应电势Eφ有效值表达式为:
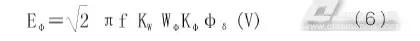
式(6)中,f为频率,KW为绕组系数,Wφ为每相串联匝数,Kφ为波形系数,φδ为每极气隙磁通量。
设Iφ为相电流的有效值,它与Eφ之间的夹角(内功率因数角)为ψ,则每相功率PEφ可求:
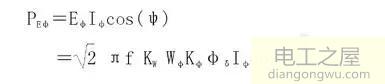
当电机按矢量控制状态运行使cos(ψ)=1时得:

对于PMSM电机,其整机的电磁功率PE可求:
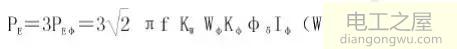
设电机的转速为n(r/min),则对应的角速度ωr可求:
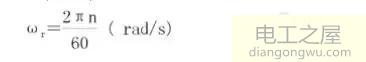
2.3.2反电势常数推导
相反电势常数KEφ可求:
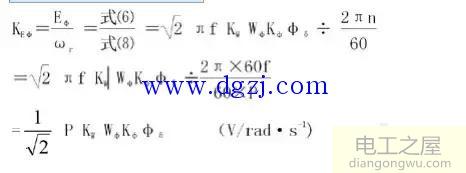
GB/T30549-2014的标准要求是线反电势常数,即:

2.3.3转矩常数推导
整机的电磁转矩Te可求:

2.3.4转矩常数与反电势常数的比值问题:
当三相绕组采用△接时:

至此,GB/T30549-2014中关于结论的推导演算完毕。
由于2014年前的标准对两常数的定义比较模糊,标准之间甚至存在相互矛盾之处,这就使两常数计算时出现这样的问题:用线值还是用相值?用有效值还是用峰值?于是各取所需出现混乱,似乎都有根据,所以国内有的伺服电机厂商提供了定义或单位不统一的两个常数,客户应用容易出错。另外,在中国市场上出现的一些国外品牌ACServo,其反电势常数与GB/T30549-2014的定义不同,基本上是按照相反电势来定义而并非采用线反电势来定义。所以我们在建议各电机厂商按照国标要求规范提供这两常数的同时,还在下面提出相关处理方法,帮助客户利用GB/T30549-2014关于转矩常数Kt和反电势常数Ke的定义,结合工程应用,更方便地读懂电机厂商提供的电机参数。
装备制造业所用ACServo中,绕组大多采用Y接(以下同),假设按照相反电势来定义的反电势常数为Keφ,则有:

式(5)和式(16)可以非常方便用于判定电机厂商提供的反电势常数的正确含义。
工程应用中常采用V/krpm为单位的反电势常数Ken。由式(4),Ke=0.00955Ken,得:
Kt/Ken=Kt/(Ke/0.00955)=0.00955×Kt/Ke=0.00955×≈0.0165(17)
3.样本数据的验证及应用
下面用几个实例来说明如何判定电机厂商提供的两个常数的定义方法,对其使用做到心中有数。
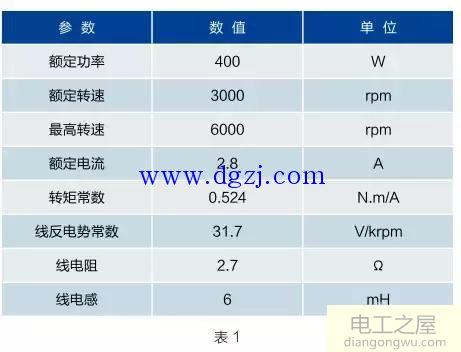
例题1:雷赛公司ACServo型号
ACM6004L2H-A0-B-HS样本数据如下(200V)如表1所示。
按照式(4),得:
Ke=0.00955×31.7=0.30273(V/rad·s-1),得:
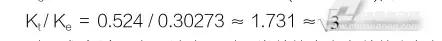
对照式(5)可知,该产品对两常数的定义在数值上与标准的规定相吻合,是因为反电势和电流都使用了线有效值。
另外,在工程应用中,转速n(r/min)、转矩TN(N.m)、功率P(W)三个参数关系如下:
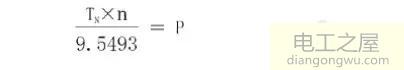
由式(18),得到本电机额定转矩为:
TN=P×9.5493/n=400×9.5493/3000=1.273(N.m)
由式(1),得电磁转矩为:
Te=Kt×IN=0.524×2.8=1.467(N.m)
由式(2)得:
T0=Te-TN=1.467-1.273=0.194(N.m)
例题2:DELTA(台达)ACServo型号ECMA-C0604样本数据如下(200V)如图2所示。
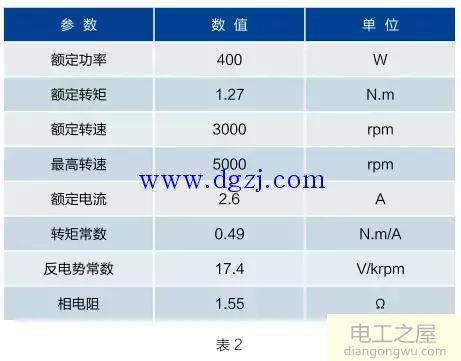
按照式(4)得:
Ke=0.00955×17.4=0.1662(V/rad·s-1),故:
Kt/Ke=0.49/0.1662=2.948≈3,可知采用了式(16)的定义,说明本电机Ke所用反电势为相电势有效值。
由式(1),得电磁转矩为:
Te=Kt×IN=0.49×2.6=1.274(N.m)
由式(2)得:
T0=Te-TN=1.274-1.27=0.004(N.m)
计算结果是额定电流产生的电磁转矩(1.274)与额定转矩(1.27)基本相同,空载转矩约等于0,数据必然存在问题,需要电机厂商分析。
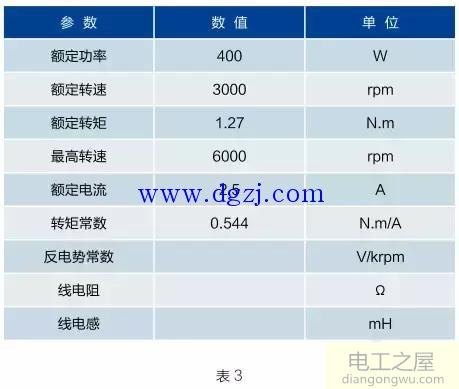
例题3:安川ACServo型号SGM7J-04A样本数据如下(200V)如表3所示。
上表未能提供反电势常数值,我们可以利用式(17)初步计算,得:
Ken=Kt/0.0165=0.544/0.0165=32.97(V/krpm)
初步验证如下:已知电机最高转速为6krpm,则在电机最高转速时的反电动势为:
Emax=Ken×nmax=32.97×6=197.82(V)
例题4:国内某品牌M公司一台60机座ACServo参数表(220V)如表4所示。表中列举的是三款同转速不同功率的电机,现来分析一下表中两个常数的可靠程度。
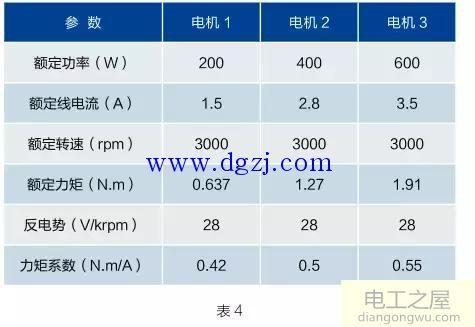
首先,由表值,用式(1)算得三种电机的电磁转矩分别为0.63、1.4、1.925(N.m),而它们相对应的额定转矩分别为0.637、1.27、1.91(N.m),并未表现出电磁转矩明显大于额定转矩的规律,让人不解;
其次,三种电机转矩常数依次是0.42、0.5、0.55(N.m/A),按照式(17),各种型号ACServo的Kt/Ken值应该是相同的,因此,不同的转矩常数,(https://www.dgzj.com/ 电工之家)其对应的反电势常数也必然不同,但表中的对应值全部都是28V/krpm,这显然丧失了样本数据的可信度。
笔者发现其它一些电机厂商也存在类似问题,这些问题的解决有待电机厂商的工作改进。
伺服驱动系统的效率测试比较方便,但单独测试ACServo的效率,需要能测算出驱动器的损耗,这比较麻烦。
可以用以下方法估算ACServo的效率。
例题5:请问例题2所述电机的效率是多少?
解:可以用以下方法估算伺服电机的效率。
电机输出功率:P2=400W
电磁功率:Pe=3(I×Eφ)=3(I×Kenφ×n)=3(2.6×17.4×3)=407.16(W)
式中:Eφ为相反电势;Kenφ为相反电势常数。
绕组铜耗:PCU=3(I2×Rφ)=3×(2.62×1.55)=31.43(W)
电机杂散损耗按1.5%估算:
PZ=P2×1.5%=400×1.5%=6(W)
电机输入功率:
P1=Pe+PCU+PZ=407.16+31.43+6=444.56(W)
因此电机效率为:
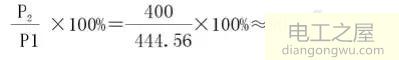
注:上述估算不包括控制器的损耗。
4.结语
(1)由于GB/T30549-2014之前的标准对两常数的定义比较模糊,标准之间甚至存在相互矛盾之处,这就使两常数计算时出现这样的问题:用线值还是用相值?用有效值还是用峰值?于是各取所需出现混乱,似乎都有根据,导致了部分电机厂商提供的两常数存在问题或矛盾,用户使用也较困惑,而且容易出错。
(2)通过前述的推导演算可知,GB/T30549-2014所述“转矩常数……在规定条件下,电机通入单位线电流时所产生的平均电磁转矩”其中提到的单位电流系有效值电流,转矩常数与反电势常数的比值为常数,通过测量确定出前者就可以计算出后者,反之亦然。所以,贯彻GB/T30549-2014标准后,处理两常数问题变得十分简单,而且不需要考虑电机绕组的具体接法。
考虑到工程应用现状,在反电势常数计算中也可以采用V/krpm为单位的反电势常数Ken,客户利用式(4),就可以方便地得到以国际单位制为单位的Ke(V/rad·s-1)。
(3)电机厂商在测试计算转矩常数的时候,要避免错误地把测功机上得到的额定转矩当做电磁转矩并用于转矩常数的计算。额定转矩加上一个空载损耗转矩(T0)才近似得到电磁转矩(Te)。