x(n)=s(n)+ r0(n),n=0,…,N-1 (2)
式(2)中s(n)是确定性信号回波,而r0(n)是随机信号。在上述模型中随机信号r0(n)的均值为零,从而可以利用波形平均的方法对x(n)进行滤波。该方法满足MSE准则,即先对x(n)进行相干叠加,再对叠加的结果求平均,来消除x(n)中的随机性信号r0(n),而保留目标的回波信号s(n),表达式如下:
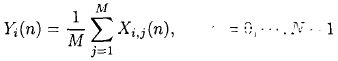 (3)
(3)
式中Xi,j(n)为在每一测量位置重复测量M 次的SPR二维剖面数据,i是测量位置的序号,通常称为道数,j是重复测量的序号;Yi(n)是经波形平均输出的UWB-SPR二维剖面数据。式(3)处理结果的误差e(n)满足MSE准则,即
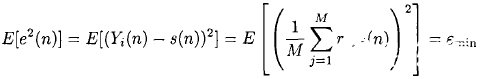 (4)
(4)
式(3)适用于系统重复频率较高时,在每道测量中做平均处理,而不是对道间数据的平均处理,这是因为SPR的回波信号随着道而变化,道间数据的平均运算将降低回波信号的能量。
3.2、中值滤波算法
中值滤波算法是对一窗口内所有数据按幅值大小进行排序,取排序后序列的中间值作为原窗口中心数据的幅值;只要选取一个有效的窗口宽度,就可以对UWB-SPR二维的剖面数据序列组,进行平滑处理,消除序列中的异常部分,抑制掉峰值噪声。中值滤波尤其适用于脉冲噪声的抑制;而GSM 的随机射频干扰信号具有窄脉冲的特性,可用中值滤波的方法有效去除回波信号中的异常部分,且能较好地保护原始回波信号。中值滤波器具有低通滤波的特性,窗口的选取有较大的影响,要保证完全去除窄带脉冲干扰,中值滤波器数据窗的宽度必须大于脉冲干扰时宽τ的2倍。窗口宽度太小,噪声抑制不彻底;窗口宽度太大,运算量较大,影响处理速度。